Kennst du das Geheimnis für schnelle und einfache Berechnungen? Es ist kein Taschenrechnerzauber, sondern der Dreisatz! Stell dir vor, du könntest im Handumdrehen Preise vergleichen, Rezepte anpassen oder die benötigte Menge an Material für dein Projekt berechnen. Mit dem Dreisatz ist das kein Problem!
Der Dreisatz ist ein mächtiges Werkzeug, das dir in vielen Situationen das Leben erleichtert. Egal ob im Alltag, im Beruf oder in der Schule – mit dieser einfachen Rechenmethode sparst du Zeit und Nerven. Dieser Artikel enthüllt die Geheimnisse des Dreisatzes und zeigt dir, wie du ihn effektiv anwenden kannst.
Was genau ist der Dreisatz und wie funktioniert er? Ganz einfach: Der Dreisatz hilft dir, unbekannte Größen zu berechnen, indem du von bekannten Verhältnissen ausgehst. Du brauchst nur drei Werte, um den vierten zu ermitteln. Klingt kompliziert? Keine Sorge, es ist einfacher als du denkst!
Die Grundlage des Dreisatzes bildet die Proportionalität. Zwei Größen sind proportional zueinander, wenn sie sich im gleichen Verhältnis ändern. Das bedeutet, wenn die eine Größe zunimmt, nimmt auch die andere zu – und umgekehrt. Diese Beziehung ist der Schlüssel zum Verständnis und zur Anwendung des Dreisatzes.
In diesem Artikel lernst du Schritt für Schritt, wie du den Dreisatz anwendest, welche Varianten es gibt und welche typischen Fehler du vermeiden solltest. Wir zeigen dir praktische Beispiele aus dem Alltag und geben dir wertvolle Tipps und Tricks, damit du zum Dreisatz-Profi wirst.
Die Geschichte des Dreisatzes reicht weit zurück. Bereits in alten babylonischen Texten finden sich Hinweise auf ähnliche Rechenmethoden. Im Laufe der Jahrhunderte wurde der Dreisatz immer weiterentwickelt und ist heute ein unverzichtbares Werkzeug in Mathematik und vielen Anwendungsbereichen.
Der Dreisatz ist im Wesentlichen eine Methode, um Proportionen zu lösen. Man geht von drei bekannten Werten aus und berechnet damit den vierten, unbekannten Wert. Ein klassisches Beispiel: Wenn 3 Äpfel 1 Euro kosten, wie viel kosten dann 6 Äpfel? Mit dem Dreisatz lässt sich diese Frage leicht beantworten.
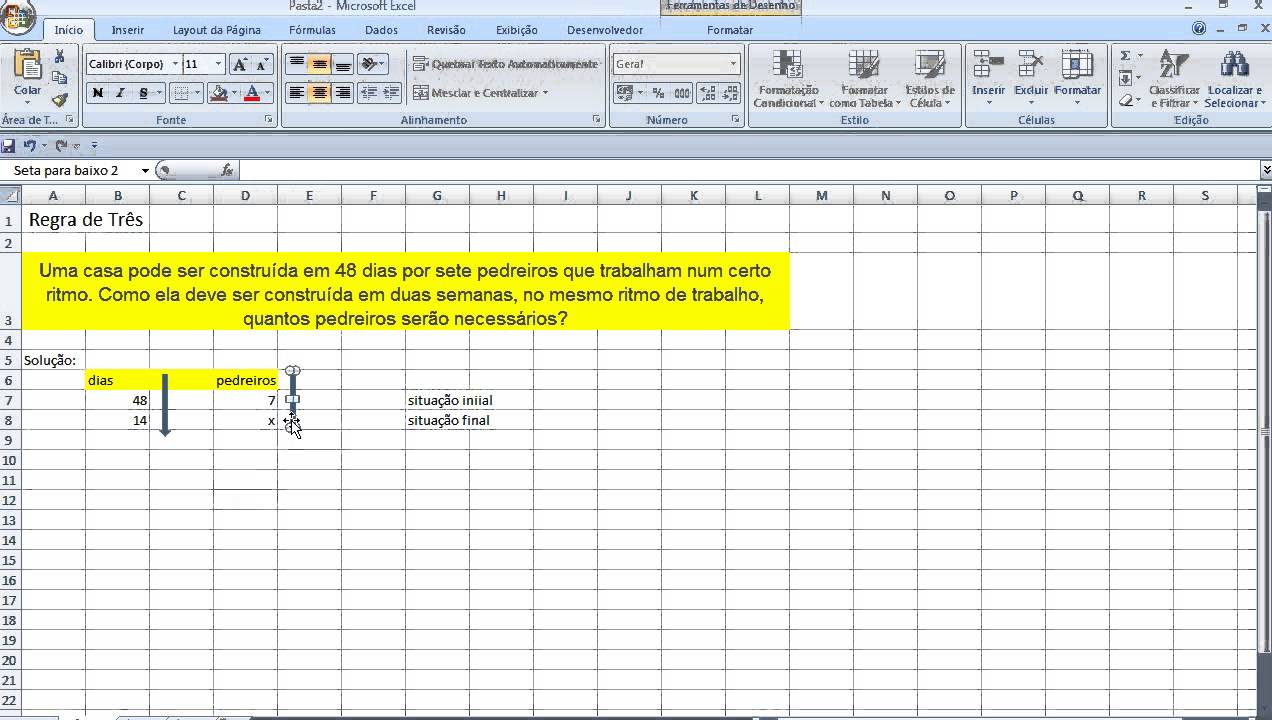
Es gibt zwei Varianten des Dreisatzes: den geraden und den ungeraden Dreisatz. Beim geraden Dreisatz steigen oder fallen die Werte im gleichen Verhältnis. Beim ungeraden Dreisatz verhält es sich umgekehrt: Steigt der eine Wert, fällt der andere.
Vorteile des Dreisatzes:
1. Einfach zu verstehen und anzuwenden.
2. Vielseitig einsetzbar in verschiedenen Bereichen.
3. Schnelle und effiziente Berechnung von unbekannten Werten.
Beispiel: 5 kg Kartoffeln kosten 2 Euro. Wie viel kosten 10 kg? Lösung: (10 kg * 2 Euro) / 5 kg = 4 Euro.
Häufig gestellte Fragen:
1. Was ist der Dreisatz? - Eine Rechenmethode zur Berechnung von Proportionen.
2. Wann verwende ich den Dreisatz? - Bei proportionalen Verhältnissen.
3. Was ist der Unterschied zwischen geradem und ungeradem Dreisatz? - Die Richtung der Proportionalität.
4. Gibt es Online-Rechner für den Dreisatz? - Ja, zahlreiche.
5. Wo finde ich weitere Übungen zum Dreisatz? - In Mathebüchern und online.
6. Wie kann ich den Dreisatz im Alltag anwenden? - Z.B. beim Kochen, Einkaufen oder beim Berechnen von Materialmengen.
7. Gibt es eine Formel für den Dreisatz? - Ja, a/b = c/x, wobei x der unbekannte Wert ist.
8. Was sind typische Fehler beim Dreisatz? - Verwechslung von geradem und ungeradem Dreisatz.
Tipps und Tricks:
Achte auf die Einheiten! Verwechsle nicht Äpfel mit Birnen – oder Kilogramm mit Gramm.
Der Dreisatz ist ein unverzichtbares Werkzeug für Berechnungen im Alltag und Beruf. Er ermöglicht es, schnell und einfach unbekannte Werte zu ermitteln, basierend auf bekannten Verhältnissen. Von der einfachen Rezeptanpassung bis hin zu komplexeren Berechnungen im Ingenieurwesen – der Dreisatz ist ein wertvoller Begleiter. Nutze die Vorteile des Dreisatzes und vereinfache deine Berechnungen! Lerne den Dreisatz und entdecke die Welt der Proportionen. Es lohnt sich!
24 zoll fernseher schnappchen auf ebay kleinanzeigen finden
Mottoparty 90er was anziehen zuruck in die zeit der coolen styles
Xml dateien in excel offnen so meistern sie die datenubertragung
oq e regra de 3 - Khao Tick On
@destruindo_no_enem @escoladenumeros - Khao Tick On
oq e regra de 3 - Khao Tick On
oq e regra de 3 - Khao Tick On
oq e regra de 3 - Khao Tick On
oq e regra de 3 - Khao Tick On
oq e regra de 3 - Khao Tick On
oq e regra de 3 - Khao Tick On
oq e regra de 3 - Khao Tick On
oq e regra de 3 - Khao Tick On
oq e regra de 3 - Khao Tick On
oq e regra de 3 - Khao Tick On
oq e regra de 3 - Khao Tick On
oq e regra de 3 - Khao Tick On
oq e regra de 3 - Khao Tick On