Geheimnis des 45-45-90 Dreiecks: Regeln und Anwendung leicht erklärt

11 Aug 2024
de
Ann

Stellen Sie sich vor, Sie schneiden einen quadratischen Kuchen diagonal durch. Was erhalten Sie? Zwei perfekte, gleichgroße Dreiecke – und genau das sind 45-45-90 Dreiecke! Sie sind überall präsent, von Architektur und Design bis hin zur Natur. Aber was macht sie so besonders? Die Antwort liegt in ihren einzigartigen Eigenschaften und der Regel, die ihre Seitenlängen bestimmt.

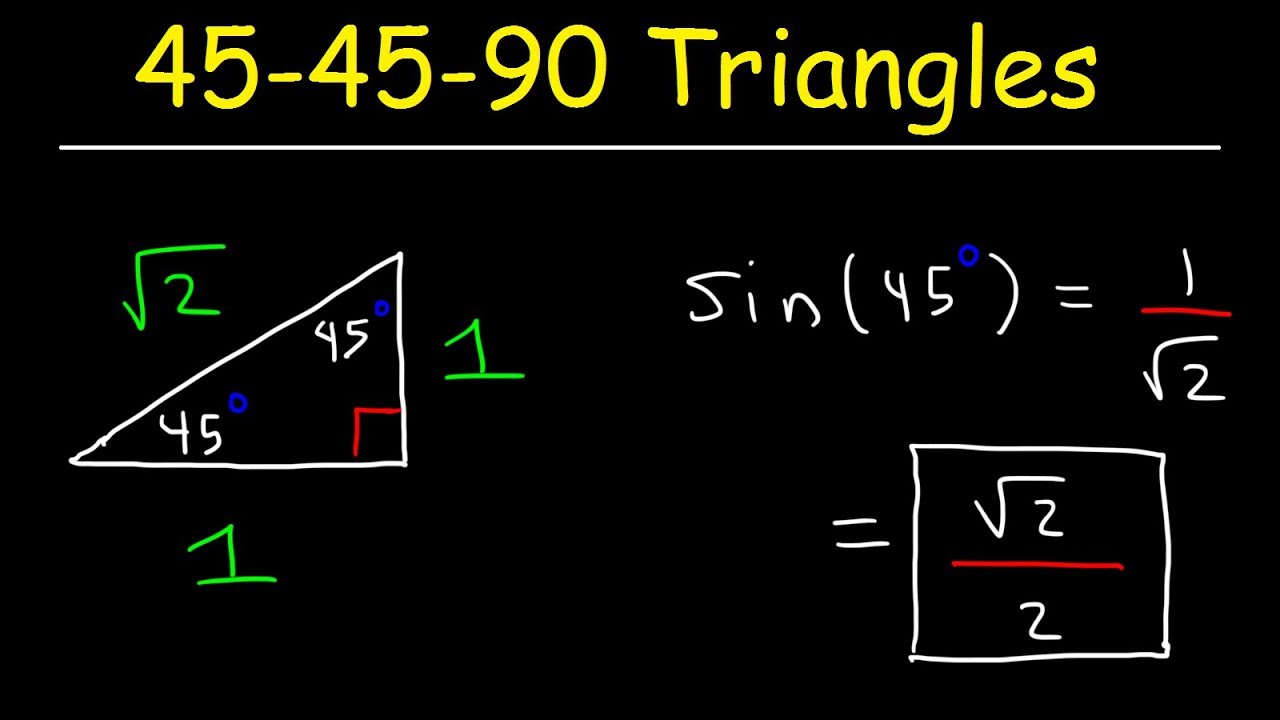
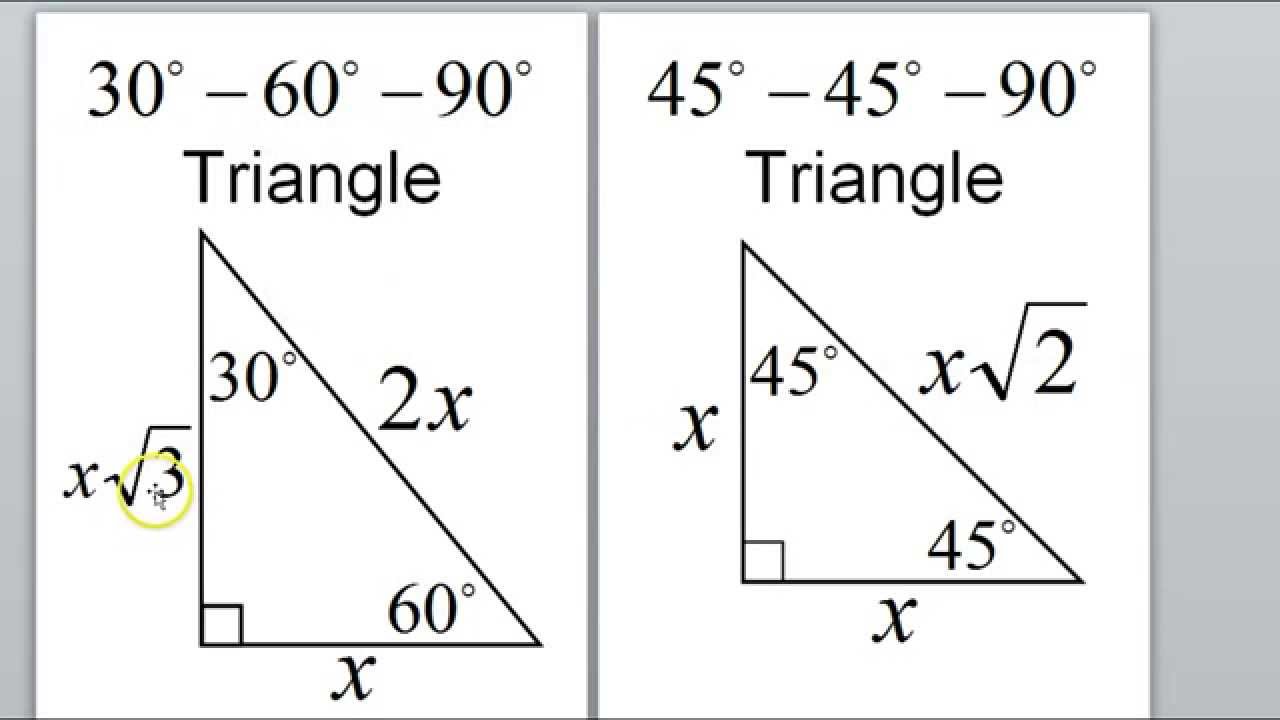
Die sogenannte "45-45-90-Regel" beschreibt das Verhältnis der Seitenlängen in diesen besonderen rechtwinkligen Dreiecken. Sie besagt, dass die beiden Katheten (die kürzeren Seiten, die den rechten Winkel bilden) gleich lang sind und die Hypotenuse (die längste Seite, gegenüber dem rechten Winkel) das √2-fache der Kathetenlänge beträgt. Diese einfache Regel eröffnet eine Welt voller Möglichkeiten zur Berechnung und Konstruktion.

Die Geschichte dieser Regel reicht weit zurück bis zu den Pythagoräern, die die Beziehung zwischen den Seiten eines rechtwinkligen Dreiecks erforschten. Das 45-45-90 Dreieck, als Spezialfall des rechtwinkligen Dreiecks, fand besondere Beachtung aufgrund seiner Symmetrie und der eleganten mathematischen Beziehung seiner Seiten. Die Bedeutung dieser Regel liegt in ihrer praktischen Anwendbarkeit, die es ermöglicht, unbekannte Seitenlängen in verschiedenen geometrischen Problemen zu berechnen.

Ein häufiges Problem beim Umgang mit 45-45-90 Dreiecken ist das Vergessen der √2-Beziehung zur Hypotenuse. Manchmal wird fälschlicherweise angenommen, dass alle Seiten gleich lang sind. Ein weiteres Problem kann das Verständnis der Anwendung der Regel in komplexeren geometrischen Figuren sein, in denen 45-45-90 Dreiecke eingebettet sind.

Die Anwendung der 45-45-90-Regel ist denkbar einfach. Wenn Sie die Länge einer Kathete kennen, multiplizieren Sie diese mit √2, um die Länge der Hypotenuse zu erhalten. Umgekehrt, wenn Sie die Länge der Hypotenuse kennen, teilen Sie diese durch √2, um die Länge der Katheten zu bestimmen. Diese Regel vereinfacht Berechnungen in vielen Bereichen, von der Geometrie über die Trigonometrie bis zur Physik.

Vorteile der Kenntnis der 45-45-90-Regel:

1. Vereinfachte Berechnungen in rechtwinkligen Dreiecken: Die Regel ermöglicht schnelle und einfache Berechnungen von Seitenlängen, ohne komplizierte trigonometrische Funktionen verwenden zu müssen.

2. Verständnis geometrischer Beziehungen: Die Regel hilft, die Zusammenhänge zwischen Seitenlängen und Winkeln in rechtwinkligen Dreiecken besser zu verstehen.

3. Praktische Anwendung in verschiedenen Bereichen: Von der Konstruktion bis zur Navigation, die 45-45-90-Regel findet in vielen Bereichen Anwendung.

Beispiel: Ein 45-45-90 Dreieck hat eine Kathete von 5 cm Länge. Die Hypotenuse ist dann 5 * √2 cm ≈ 7,07 cm lang.

Häufig gestellte Fragen:

1. Was ist ein 45-45-90 Dreieck? Ein rechtwinkliges Dreieck mit zwei gleich langen Katheten und Basiswinkeln von 45 Grad.

2. Wie lautet die 45-45-90-Regel? Kathete * √2 = Hypotenuse.

3. Wo finde ich 45-45-90 Dreiecke im Alltag? In Architektur, Design, Kunst und Natur.

4. Wie kann ich die Regel anwenden? Um unbekannte Seitenlängen in 45-45-90 Dreiecken zu berechnen.

5. Was ist der Satz des Pythagoras? a² + b² = c² (für alle rechtwinkligen Dreiecke).

6. Wie hängen der Satz des Pythagoras und die 45-45-90-Regel zusammen? Die 45-45-90-Regel ist ein Spezialfall des Satzes des Pythagoras.

7. Warum ist die Kenntnis dieser Regel wichtig? Sie vereinfacht Berechnungen in vielen Bereichen.

8. Gibt es Online-Ressourcen zum Thema? Ja, zahlreiche Websites und Lernvideos bieten weitere Informationen.

Zusammenfassend lässt sich sagen, dass die 45-45-90-Regel ein mächtiges Werkzeug ist, das uns hilft, die Welt der Geometrie besser zu verstehen und komplexe Probleme elegant zu lösen. Von der einfachen Berechnung von Seitenlängen bis hin zur Anwendung in Architektur und Design, die Kenntnis dieser Regel ist unerlässlich für jeden, der sich mit Mathematik und ihren Anwendungen auseinandersetzt. Nutzen Sie die Vorteile dieser Regel und entdecken Sie die faszinierende Welt der 45-45-90 Dreiecke!

Vollmacht formular zum ausdrucken kostenlos so einfach gehts
Wie alt wird eine eule geheimnisvolle jager der nacht
Tages gruesse bilder kostenlos