Décrypter le Monde : La Représentation Graphique de la Régression

10 Jul 2024
fr
Ann

comment tracer un graphique sur regressi

Dans un monde inondé de données, la capacité à donner un sens aux chiffres est devenue une compétence essentielle. La représentation graphique de la régression, en particulier, offre une fenêtre puissante sur les relations complexes qui sous-tendent les ensembles de données. Plus qu'un simple outil statistique, elle permet de révéler des tendances, de prévoir des résultats et de prendre des décisions éclairées.

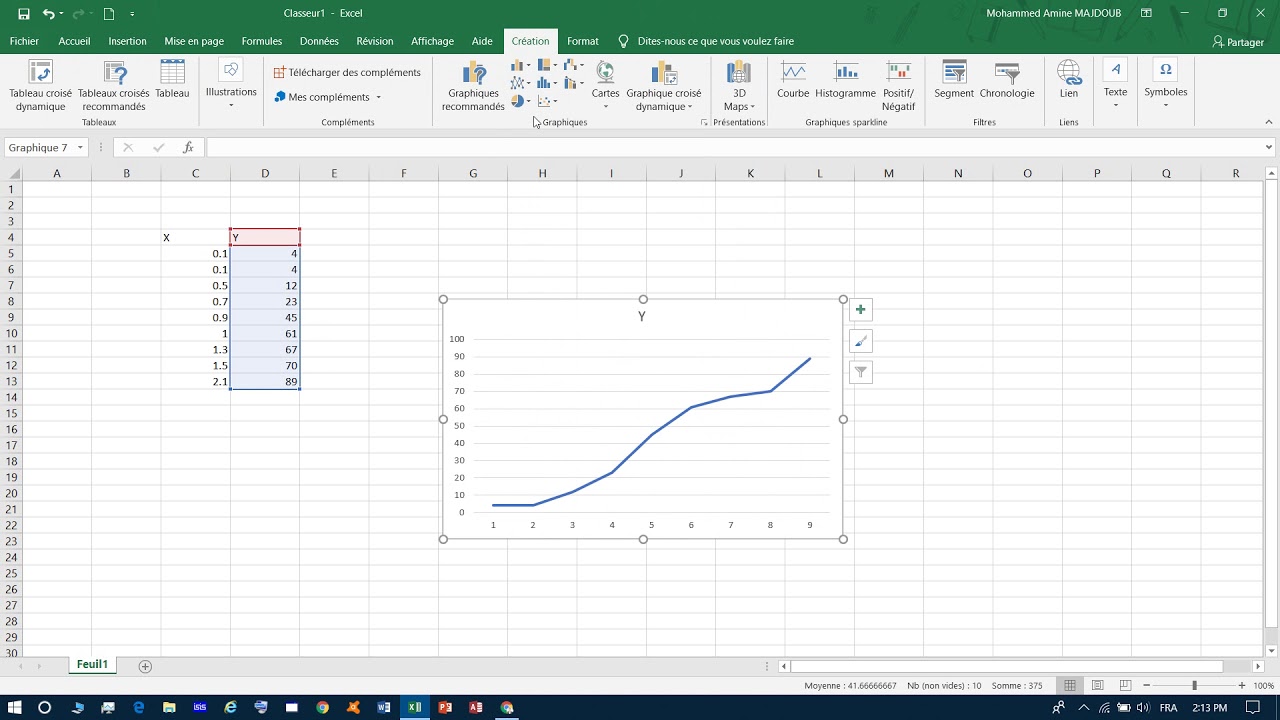
Mais comment fonctionne exactement la représentation graphique de la régression ? Imaginez un nuage de points représentant des données, chaque point symbolisant une observation. La représentation graphique de la régression consiste à tracer une droite (ou une courbe) à travers ces points, capturant ainsi au mieux la relation globale. Cette droite, appelée droite de régression, permet de visualiser la tendance générale des données et de faire des prédictions pour des valeurs non observées.

L'histoire de la représentation graphique de la régression remonte aux travaux pionniers de Sir Francis Galton au XIXe siècle. En étudiant la relation entre la taille des parents et celle de leurs enfants, Galton a constaté que la taille des enfants tendait à "régresser" vers la moyenne de la population. Cette observation a conduit au développement de l'analyse de régression, qui est rapidement devenue un outil indispensable dans de nombreux domaines, de l'économie à la médecine en passant par les sciences sociales.

Aujourd'hui, la représentation graphique de la régression est largement utilisée pour explorer et comprendre les relations entre les variables. Par exemple, un économiste peut l'utiliser pour étudier l'impact des dépenses publicitaires sur les ventes, tandis qu'un médecin peut l'utiliser pour analyser la relation entre l'indice de masse corporelle et le risque de maladie cardiaque. La polyvalence de cet outil en fait un atout précieux pour toute personne cherchant à extraire des informations significatives à partir de données.

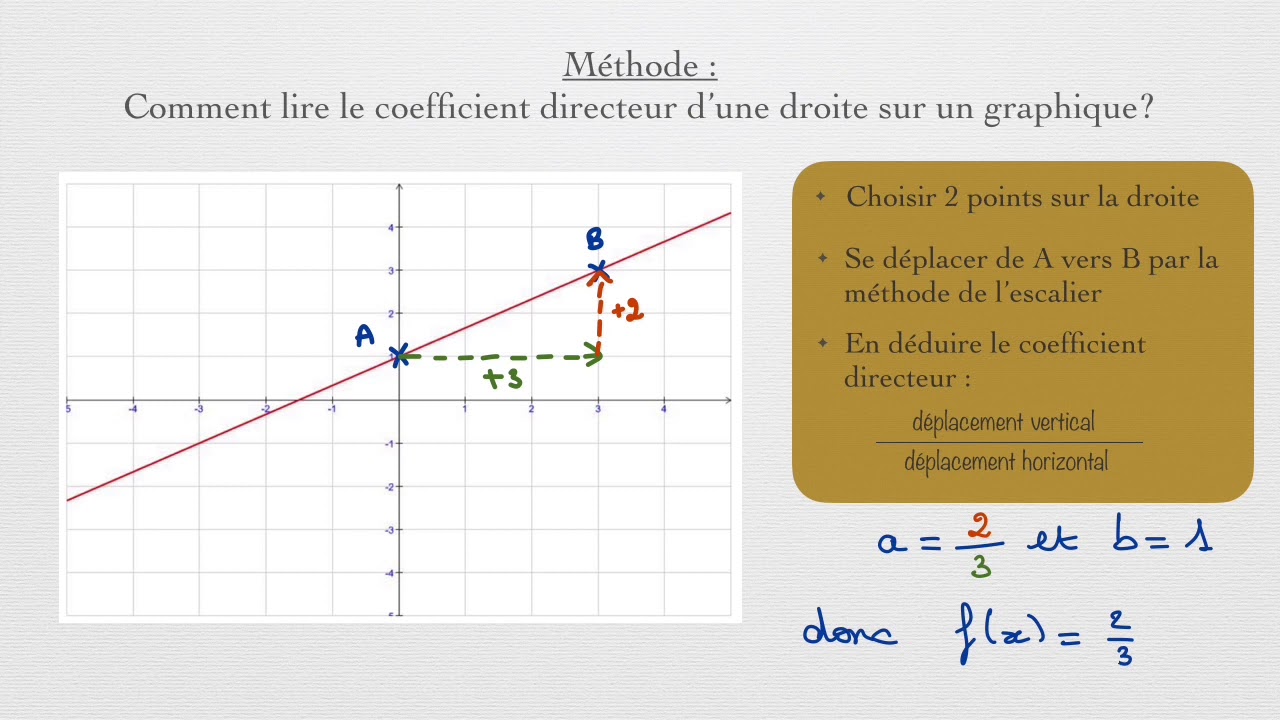
L'un des principaux avantages de la représentation graphique de la régression réside dans sa capacité à visualiser des tendances qui pourraient ne pas être immédiatement apparentes dans un tableau de chiffres. En représentant graphiquement les données, nous pouvons rapidement identifier les relations positives ou négatives, ainsi que la force de ces relations. La pente de la droite de régression nous indique la direction de la relation, tandis que le coefficient de détermination (R²) nous donne une mesure de la qualité de l'ajustement de la droite aux données.

En conclusion, la représentation graphique de la régression est un outil puissant qui permet de donner un sens aux données et de prendre des décisions plus éclairées. En révélant les relations cachées entre les variables, elle ouvre la voie à une meilleure compréhension du monde qui nous entoure. Qu'il s'agisse d'étudier les tendances économiques, de faire progresser la recherche médicale ou simplement de mieux comprendre les données qui façonnent nos vies, la représentation graphique de la régression s'avère être un outil précieux à l'ère de l'information.

Lafrique du sud joyau du continent africain
Sucre dorge dessin png
Benjamin franklin un genie aux multiples casquettes