Dans l'univers fascinant de l'analyse des données, un concept fondamental se dresse : les échelles de mesure des variables. Imaginez, un instant, vouloir comprendre le monde qui vous entoure, quantifier les phénomènes, déceler les tendances cachées... C'est là que les échelles de mesure entrent en jeu, telles des clés pour déverrouiller les secrets des données.
Mais qu'est-ce qu'une échelle de mesure, au juste ? C'est une manière de classifier les variables en fonction de leurs propriétés mathématiques. On peut les voir comme des règles du jeu qui déterminent les opérations possibles et les interprétations que l'on peut faire des données. Choisir la bonne échelle est crucial, car une échelle inadaptée peut fausser l'analyse et conduire à des conclusions erronées.
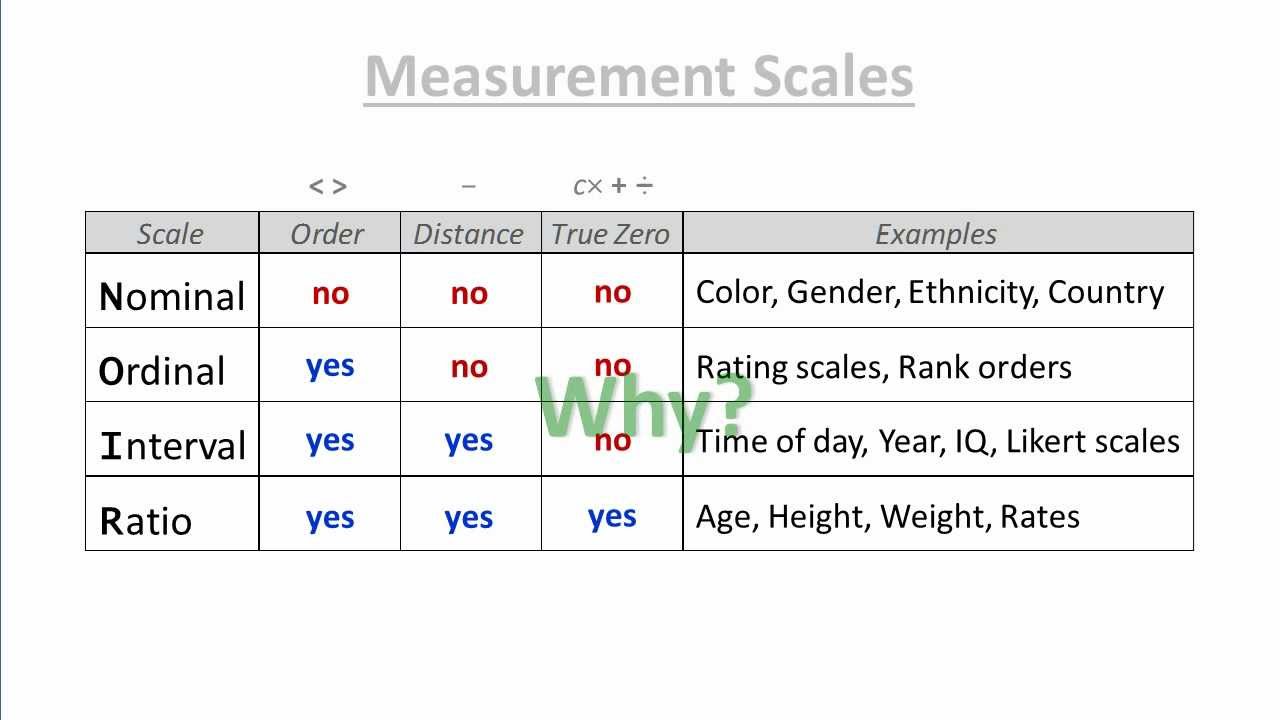
L'histoire des échelles de mesure remonte aux travaux pionniers de Stanley Smith Stevens, un psychologue américain qui, dans les années 1940, a proposé une classification qui reste aujourd'hui une référence. Il a distingué quatre niveaux de mesure : nominale, ordinale, d'intervalle et de rapport. Cette classification a permis de structurer la manière dont les données sont collectées et analysées, ouvrant la voie à des analyses plus rigoureuses et plus pertinentes.
L'importance des échelles de mesure est donc capitale. Elles permettent de choisir les méthodes statistiques appropriées. Par exemple, on ne peut pas calculer une moyenne sur des données nominales, comme les couleurs de cheveux, alors que c'est possible sur des données d'intervalle, comme les températures. Comprendre ces nuances est essentiel pour éviter les erreurs d'interprétation et tirer des conclusions fiables.
Cependant, l'utilisation des échelles de mesure n'est pas sans poser quelques défis. Un des problèmes récurrents est la confusion entre les différents niveaux de mesure. Par exemple, certains pourraient être tentés de traiter des données ordinales, comme les niveaux de satisfaction (très satisfait, satisfait, insatisfait), comme des données d'intervalle, en leur attribuant des valeurs numériques arbitraires. Cette pratique peut conduire à des conclusions erronées, car l'écart entre "très satisfait" et "satisfait" n'est pas forcément le même qu'entre "satisfait" et "insatisfait".
Prenons l'exemple du niveau de satisfaction client. On peut utiliser une échelle nominale (satisfait/insatisfait), ordinale (très satisfait/satisfait/insatisfait), ou d'intervalle (note de 1 à 10). Chaque échelle offre un niveau de détail différent et permet des analyses différentes.
Les échelles de mesure offrent de nombreux avantages. Elles permettent de structurer les données, de choisir les méthodes statistiques appropriées et d'interpréter les résultats de manière rigoureuse. Elles sont essentielles pour mener des analyses quantitatives et qualitatives fiables.
Pour mettre en œuvre les échelles de mesure, il est important de bien définir les variables, de choisir l'échelle la plus appropriée en fonction du type de données et de l'objectif de l'étude, et de documenter les choix effectués pour assurer la transparence et la reproductibilité de l'analyse.
Parmi les questions fréquemment posées, on retrouve : Quelle échelle utiliser pour mesurer la taille ? (échelle de rapport). Quelle échelle pour les couleurs ? (nominale). Comment choisir entre une échelle ordinale et d'intervalle ? Et bien d'autres encore...
En conclusion, les échelles de mesure des variables sont des outils fondamentaux pour l'analyse des données. Elles permettent de structurer l'information, de choisir les méthodes statistiques appropriées et d'interpréter les résultats de manière rigoureuse. Maîtriser les échelles de mesure est essentiel pour quiconque souhaite explorer le monde des données et en tirer des conclusions pertinentes. N'hésitez pas à approfondir vos connaissances sur ce sujet pour améliorer vos compétences en analyse de données.
Nike off white mca price le graal des sneakers
Lheritage visuel de sonic adventure dx une illustration emblematique
Decryptage de la courbe de croissance du bebe allaite
scales for measurement of variables - Khao Tick On
What Is Nominal Ordinal Interval Ratio - Khao Tick On
Nominal Ordinal Interval Ratio Scales - Khao Tick On
What is the difference between ordinal interval and ratio variables - Khao Tick On
Variables And Measurement Scales - Khao Tick On
Measurement Scales Nominal Ordinal Interval Ratio Statistics Images - Khao Tick On
Nominal Ordinal Interval Ratio Examples - Khao Tick On
scales for measurement of variables - Khao Tick On
Chapter 24 Describing Employee Demographics Using Descriptive - Khao Tick On
scales of measurement statistics test chart Types measurement scales - Khao Tick On
scales for measurement of variables - Khao Tick On
What are the scales of measurement - Khao Tick On
scales for measurement of variables - Khao Tick On
scales for measurement of variables - Khao Tick On
What Is Variable Interval - Khao Tick On