Vi siete mai trovati di fronte a un problema matematico che sembrava un enigma impossibile da risolvere? Capita a tutti, specialmente quando si ha a che fare con i sistemi di equazioni. Ma cosa succederebbe se vi dicessi che esiste un metodo semplice e intuitivo per trovare la soluzione? In questa guida, esploreremo il mondo della risoluzione grafica dei sistemi di equazioni, un approccio visivo che può rendere la matematica molto più accessibile.
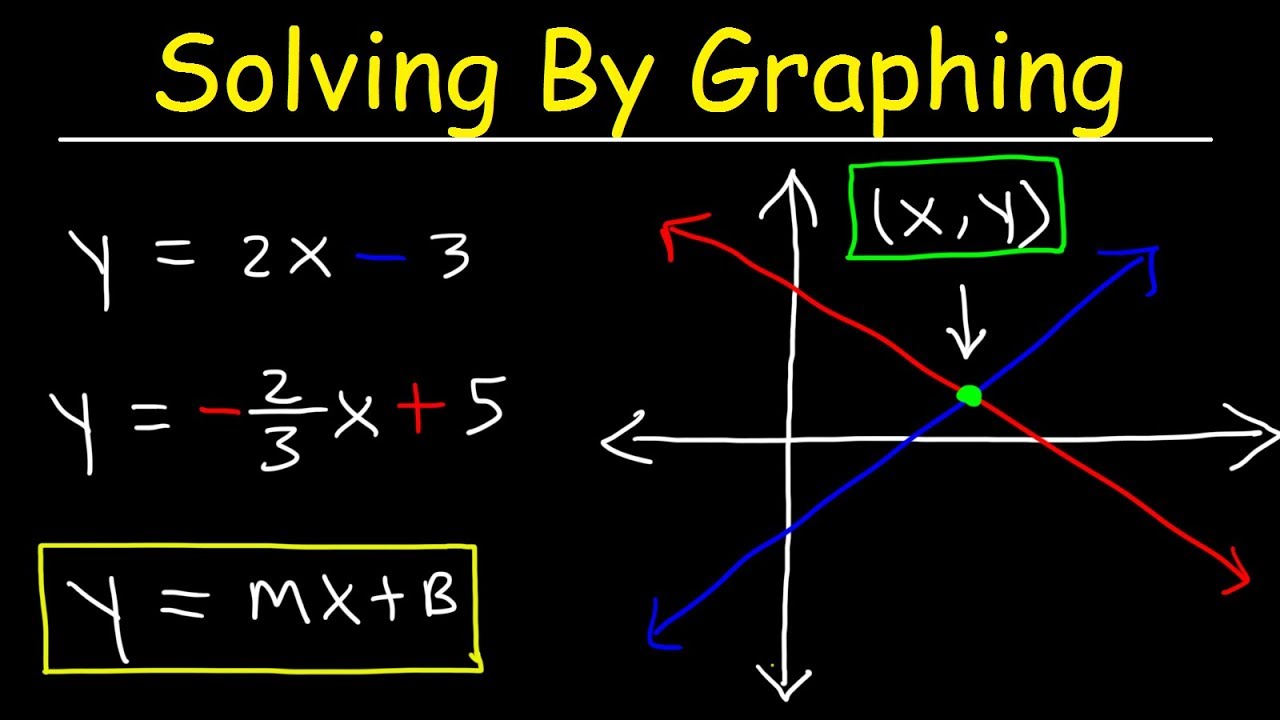
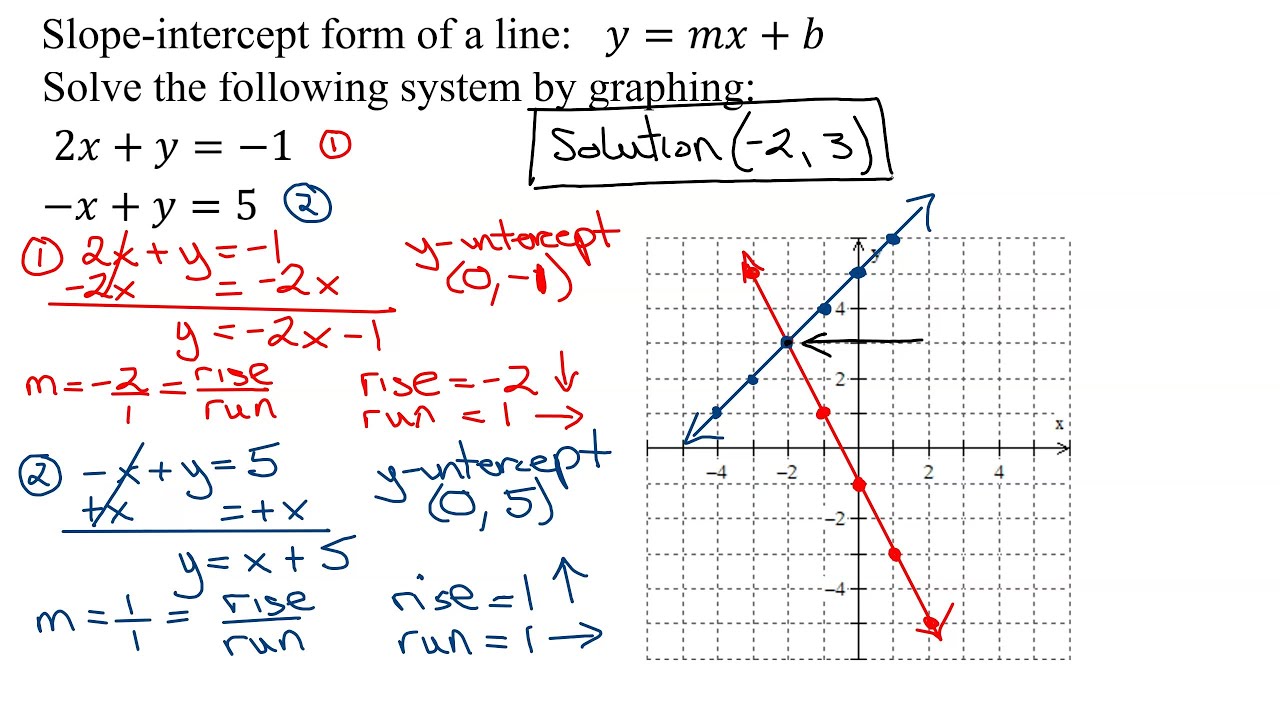
Immaginate di avere due linee rette disegnate su un grafico. Ognuna di queste linee rappresenta un'equazione con due variabili, come x e y. Il punto in cui le due linee si intersecano, se esiste, rappresenta la soluzione del sistema, ovvero i valori di x e y che soddisfano entrambe le equazioni contemporaneamente.
Questo è l'essenza della risoluzione di un sistema di equazioni attraverso il metodo grafico. Anziché manipolare algebricamente le equazioni, le rappresentiamo graficamente e cerchiamo il loro punto di intersezione. Questo approccio può essere incredibilmente utile per visualizzare il problema e comprendere il significato delle soluzioni.
La risoluzione grafica dei sistemi di equazioni ha una lunga storia, che risale agli albori della geometria analitica. Questo ramo della matematica, sviluppatosi nel XVII secolo, ha unito il rigore dell'algebra con l'intuitività della geometria, consentendo di rappresentare equazioni algebriche come figure geometriche e viceversa.
Il metodo grafico è particolarmente utile in diversi ambiti, come l'economia, l'ingegneria e la fisica, dove i sistemi di equazioni sono spesso utilizzati per modellare fenomeni reali. Ad esempio, potremmo voler trovare il punto di equilibrio tra domanda e offerta in un mercato, oppure determinare la traiettoria di un proiettile in base alla sua velocità iniziale e all'angolo di lancio. In tutti questi casi, la rappresentazione grafica può fornire una comprensione immediata e intuitiva del problema.
Vantaggi e Svantaggi della Risoluzione Grafica
| Vantaggi | Svantaggi |
|---|---|
| Intuitivo e facile da capire | Precisione limitata per soluzioni non intere |
| Permette di visualizzare il problema e la soluzione | Richiede tempo per disegnare i grafici |
| Utile per verificare le soluzioni ottenute con altri metodi | Difficile da applicare con sistemi di più di due variabili |
Sebbene la risoluzione grafica offra molti vantaggi, è importante notare alcune limitazioni. La precisione della soluzione dipende dalla cura con cui vengono disegnati i grafici. Inoltre, il metodo diventa più complesso da applicare quando si ha a che fare con sistemi di più di due equazioni o quando le soluzioni non sono numeri interi.
Nonostante queste limitazioni, la risoluzione grafica rimane un potente strumento per affrontare i sistemi di equazioni, offrendo una prospettiva unica e complementare ad altri metodi di risoluzione. Padroneggiare questo approccio può fornire una solida base per affrontare con successo problemi matematici più complessi in futuro.
Il cast indimenticabile di la grande bellezza un viaggio tra i volti di roma
Elsa e anna frozen png dove trovare le immagini perfette
Buen lunes buena semana il segreto per una settimana di successo
Solve A System By Graphing Worksheet - Khao Tick On
Solve Each System By Graphing Worksheets Answer Key - Khao Tick On
Systems By Graphing Worksheets - Khao Tick On
How To Solve Linear Equations And Graph Them - Khao Tick On
Solving Systems By Graphing Worksheet - Khao Tick On
solving each system by graphing - Khao Tick On
Graphing System Of Linear Inequalities Worksheets - Khao Tick On