Vi siete mai chiesti come fanno le aziende a capire se una nuova campagna pubblicitaria sta effettivamente aumentando le vendite? O come fanno i ricercatori a determinare se un nuovo farmaco è davvero efficace? La risposta, spesso, risiede in uno strumento statistico chiamato "Z-test". In questo articolo, esploreremo il mondo del "Z-test problem solving example", fornendo una guida completa con esempi pratici e consigli utili per padroneggiare questo potente strumento.
Immaginiamo di dover decidere se una moneta è truccata o meno. Potremmo lanciarla un certo numero di volte e annotare il numero di teste e croci. Ma come possiamo essere sicuri che i risultati ottenuti non siano dovuti al caso? È qui che entra in gioco il Z-test: ci permette di confrontare i nostri risultati con ciò che ci aspetteremmo dalla casualità e di determinare se la differenza è statisticamente significativa.
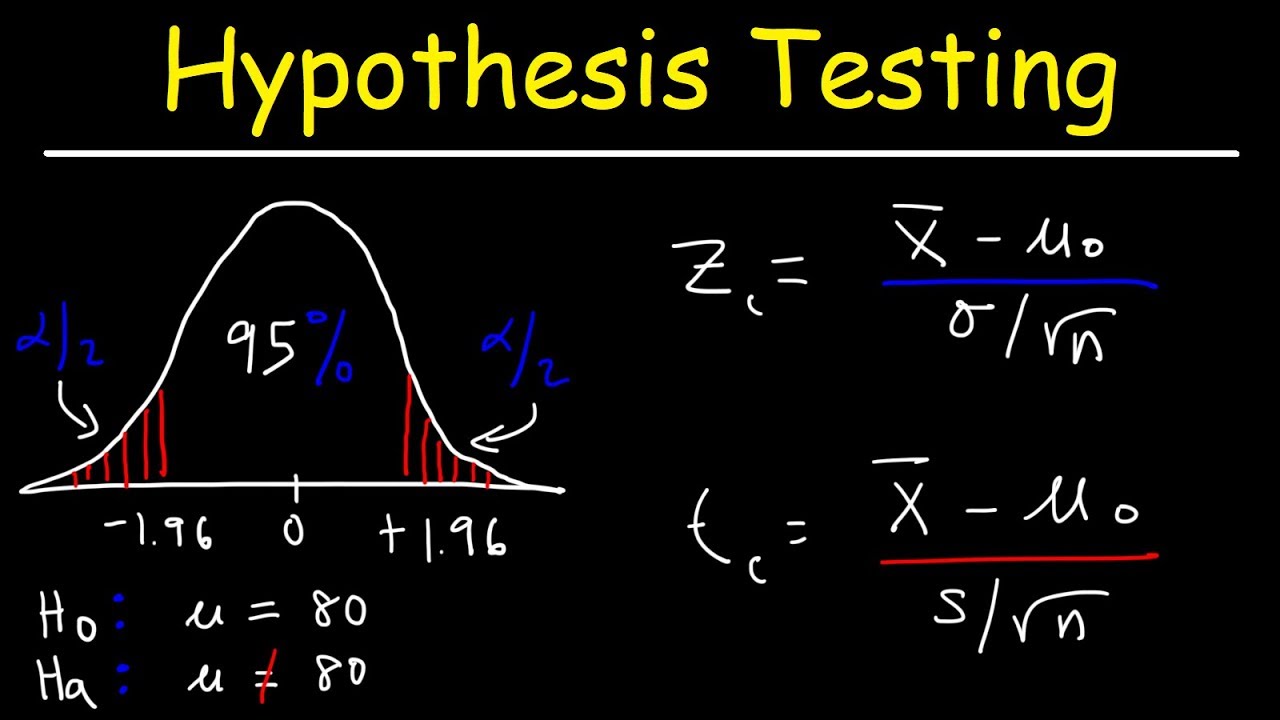
Il Z-test si basa sulla distribuzione normale standard, una curva a campana che descrive la distribuzione dei dati in molte situazioni reali. Utilizzando questa distribuzione come riferimento, il Z-test ci fornisce un valore numerico, chiamato "punteggio Z", che indica quanto i nostri dati si discostano dalla media della popolazione di riferimento. Più alto è il punteggio Z, più è probabile che la differenza osservata non sia dovuta al caso.
Ma il Z-test non si limita a testare le monete. È uno strumento versatile che trova applicazione in moltissimi ambiti: dal controllo qualità in fabbrica all'analisi dei dati di mercato, dalla ricerca medica alla psicologia sperimentale. In sostanza, ogni volta che dobbiamo confrontare due gruppi di dati e determinare se la differenza tra loro è statisticamente significativa, il Z-test può venirci in aiuto.
Per comprendere meglio il funzionamento del Z-test, vediamo un esempio concreto. Supponiamo che un'azienda voglia testare l'efficacia di un nuovo fertilizzante. A tal fine, divide un campo in due parti uguali: una trattata con il nuovo fertilizzante e l'altra con un fertilizzante standard. Dopo un certo periodo di tempo, misura la resa di entrambe le parti del campo. Per determinare se la differenza di resa è statisticamente significativa, l'azienda può utilizzare un Z-test. Il test confronterà la resa media del gruppo trattato con il nuovo fertilizzante con la resa media del gruppo di controllo e fornirà un punteggio Z. Se il punteggio Z è sufficientemente alto, l'azienda può concludere che il nuovo fertilizzante è effettivamente più efficace.
Vantaggi e Svantaggi del Z-test
Come ogni strumento statistico, il Z-test presenta sia vantaggi che svantaggi:
| Vantaggi | Svantaggi |
|---|---|
| Relativamente semplice da capire e applicare | Richiede la conoscenza della deviazione standard della popolazione, che spesso è sconosciuta |
| Ampiamente utilizzato e accettato nella comunità scientifica | Sensibile alla dimensione del campione: meno preciso con campioni piccoli |
| Utile per prendere decisioni basate sui dati in diversi ambiti | Presuppone che i dati siano distribuiti normalmente, il che potrebbe non essere sempre vero |
Nonostante i suoi limiti, il Z-test rimane uno strumento prezioso per l'analisi dei dati e il problem solving. Comprendere i suoi punti di forza e di debolezza è fondamentale per utilizzarlo in modo efficace e trarre conclusioni accurate.
Ordine dei farmacisti ravenna cosa ce da sapere
Imagenes de buenos dias jueves la mejor manera de comenzar el dia
Auguri di compleanno amica 60 anni idee speciali per un giorno indimenticabile
Top Six Sigma Problem - Khao Tick On
Brain Training FOR SMART KIDS: Matrix Reasoning Practice Book for the - Khao Tick On
College Physics, 5e Alan Giambattista (Test Bank) - Khao Tick On
One Sample T Test Example - Khao Tick On
problem solving sample test - Khao Tick On
Problem solving: 5 tecniche per imparare a risolvere i Test - Khao Tick On
Creativity and Innovation Archives - Khao Tick On
Perfect IQ Test Pro: Train Your Brain - Khao Tick On
example of problem solving organizer - Khao Tick On
Z Test For 2 Sample Means at Jeffrey Robinson blog - Khao Tick On
z test problem solving example - Khao Tick On
Venn Diagram Questions And Solutions - Khao Tick On
z test problem solving example - Khao Tick On
25 Fun Problem Solving Activities for Kids - Khao Tick On
z test problem solving example - Khao Tick On