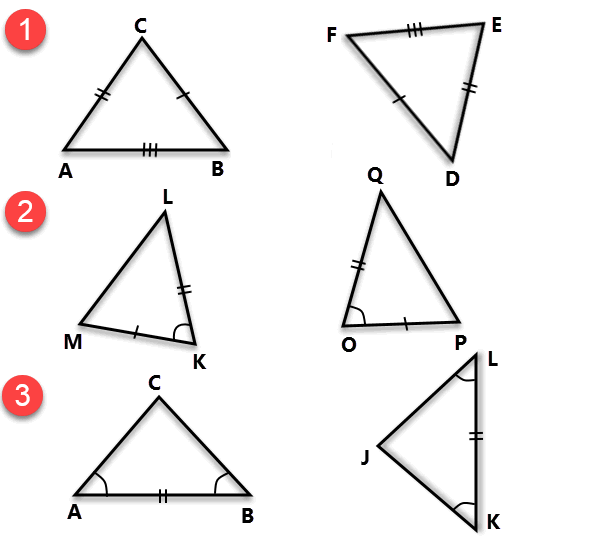
Pernahkah anda perhatikan bagaimana sesetengah bentuk geometri kelihatan sama persis? Bukan sekadar serupa, tetapi benar-benar identik dalam setiap aspek? Itulah dunia segitiga kongruen, konsep penting dalam geometri yang memainkan peranan penting dalam pelbagai bidang, dari seni bina hingga kejuruteraan.
Bayangkan anda sedang membina sebuah jambatan. Setiap bahagian struktur mestilah tepat dan kukuh. Di sinilah segitiga kongruen memainkan peranannya. Dengan memastikan segitiga yang digunakan dalam pembinaan adalah kongruen, jurutera dapat menjamin kestabilan dan kekuatan struktur tersebut.
Tetapi apa sebenarnya segitiga kongruen? Dalam istilah mudah, dua segitiga dikatakan kongruen jika mereka mempunyai saiz dan bentuk yang sama. Ini bermakna setiap sisi dan setiap sudut pada satu segitiga adalah sama dengan sisi dan sudut yang sepadan pada segitiga yang lain.
Konsep keserupaan bentuk telah lama dikaji, sejak zaman Euclid, ahli matematik Yunani kuno yang meletakkan asas geometri. Euclid mengenal pasti bahawa segitiga kongruen mempunyai sifat unik yang membolehkan kita membuat kesimpulan dan menyelesaikan masalah geometri.
Keupayaan untuk mengenal pasti dan menggunakan segitiga kongruen bukan sahaja penting dalam matematik, tetapi juga dalam pelbagai bidang lain. Daripada mereka bentuk corak jubin yang rumit hingga kepada memastikan ketepatan dalam pembuatan, pemahaman tentang segitiga kongruen membuka pintu kepada pelbagai aplikasi praktikal.
Kelebihan dan Kekurangan Segitiga Kongruen
Berikut adalah beberapa kelebihan dan kekurangan segitiga kongruen:
| Kelebihan | Kekurangan |
|---|---|
| Memudahkan pengiraan dan pembuktian dalam geometri. | Mengenal pasti segitiga kongruen mungkin rumit dalam sesetengah kes. |
| Mempunyai aplikasi praktikal dalam pelbagai bidang seperti seni bina, kejuruteraan dan reka bentuk. | Konsep ini terhad kepada segitiga dan tidak boleh diaplikasikan kepada semua bentuk geometri. |
Soalan Lazim tentang Segitiga Kongruen
Berikut adalah beberapa soalan lazim tentang segitiga kongruen:
Apakah perbezaan antara segitiga kongruen dan segitiga serupa?
Segitiga kongruen mempunyai saiz dan bentuk yang sama, manakala segitiga serupa mempunyai bentuk yang sama tetapi saiz yang berbeza.
Apakah syarat-syarat untuk dua segitiga menjadi kongruen?
Terdapat beberapa syarat, termasuk Sisi-Sisi-Sisi (SSS), Sisi-Sudut-Sisi (SAS), Sudut-Sisi-Sudut (ASA), dan Sudut-Sudut-Sisi (AAS).
Segitiga kongruen, walaupun merupakan konsep geometri yang asas, mempunyai implikasi yang mendalam dalam pelbagai bidang. Daripada memahami struktur bangunan hingga kepada menghargai keindahan corak geometri, pengetahuan tentang segitiga kongruen membuka pintu kepada pemahaman yang lebih mendalam tentang dunia di sekeliling kita. Sama ada anda seorang pelajar, seorang profesional, atau hanya ingin tahu tentang keajaiban matematik, luangkan masa untuk meneroka dunia segitiga kongruen yang menarik - anda mungkin akan terkejut dengan apa yang anda temui!
Doa setelah sholat tahajud dan artinya menggapai kedekatan dengan sang pencipta
Cara mudah tukar google docs ke word panduan lengkap anda
Pecahan power kuasai soalan membandingkan pecahan kelas 3
SOLVED: pertanyaan 1. masih ingatkah kalian dengan bangun ruang pada - Khao Tick On
Kekongruenan dan Kesebangunan.ppt - Khao Tick On
apa itu segitiga kongruen - Khao Tick On
Kunci Jawaban Buku Matematika SMP Kelas 9 Latihan 4.1 Nomor 1, 2, 3, 4 - Khao Tick On
apa itu segitiga kongruen - Khao Tick On
Jawaban Tuliskan Satu Pasangan Segitiga Kongruen Setiap Bangun Berikut - Khao Tick On
Apa Arti Dalam Matematika - Khao Tick On
OLEH: SITI NURFARISA PITRI HANDAYANI ABDUL MUHIT - Khao Tick On
apa itu segitiga kongruen - Khao Tick On
Kesebangunan dan Kekongruenan Bangun Datar dalam Matematika - Khao Tick On
apa itu segitiga kongruen - Khao Tick On
Apa Itu Segitiga Alaska? Tempat Hilangnya Lebih dari 20.000 Orang - Khao Tick On
Unik, Contek 7 Model Rumah Atap Segitiga Terbaru Ini - Khao Tick On
Contoh Soal Segitiga Kongruen - Khao Tick On
SOLVED: pertanyaan 1. masih ingatkah kalian dengan bangun ruang pada - Khao Tick On