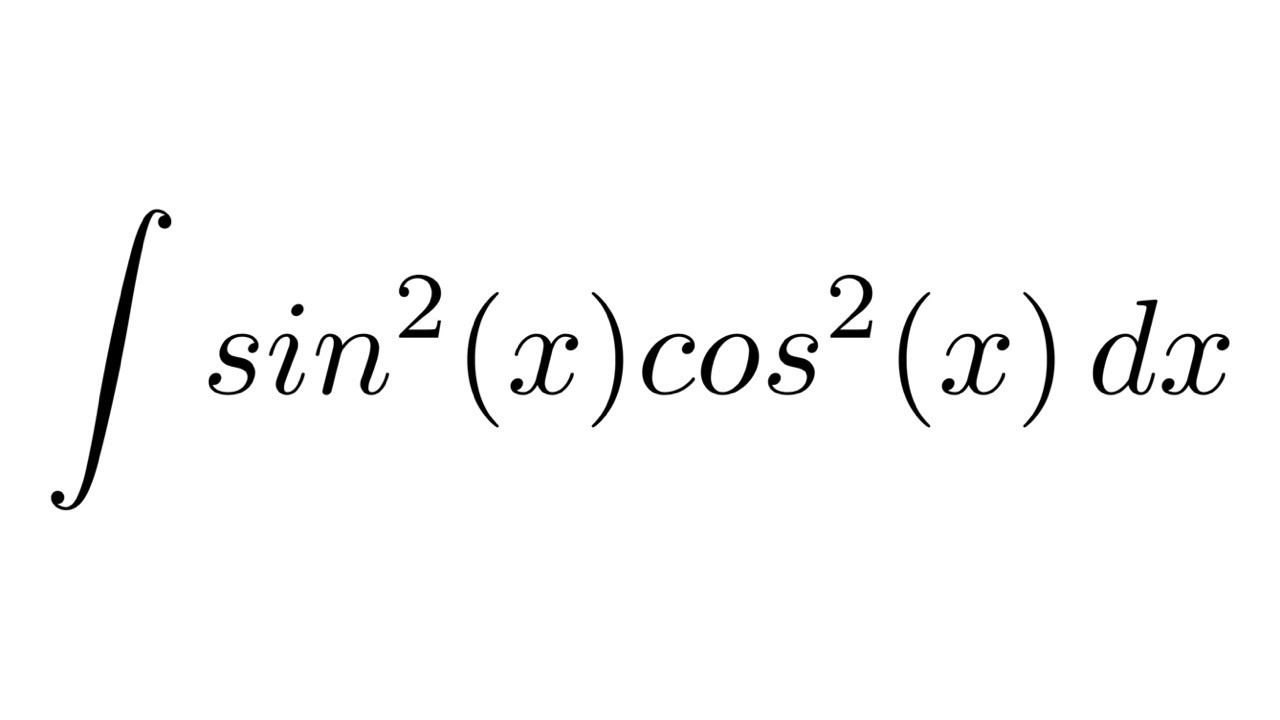Wiskunde, voor velen een wereld vol mysteriën, maar ook een bron van fascinerende ontdekkingen. Eén van die intrigerende concepten is de integraal, een krachtig hulpmiddel dat ons in staat stelt om oppervlaktes, volumes en andere complexe berekeningen te maken.
In deze wondere wereld van integralen duiken we dieper in op een specifiek geval: de integraal van sin 2x. Deze integraal, die op het eerste gezicht misschien abstract lijkt, heeft tal van toepassingen in verschillende vakgebieden, van natuurkunde tot engineering.
Maar wat maakt de integraal van sin 2x nu zo bijzonder? Wel, in tegenstelling tot de integraal van sin x, die simpelweg -cos x is, vereist de integraal van sin 2x een iets andere aanpak. Om deze te berekenen, maken we gebruik van een handige techniek genaamd substitutie, waardoor we de integraal kunnen vereenvoudigen en oplossen.
De integraal van sin 2x is echter veel meer dan alleen een wiskundige formule. Het is een concept dat deuren opent naar een dieper begrip van trigonometrische functies en hun rol in de beschrijving van periodieke verschijnselen. Denk bijvoorbeeld aan de beweging van een slinger, de oscillatie van een veer of de golfbewegingen van geluid en licht. In al deze gevallen speelt de integraal van sin 2x, en meer algemeen de integraal van trigonometrische functies, een cruciale rol.
Laten we eens kijken naar een concreet voorbeeld om dit te illustreren. Stel je voor dat je de arbeid wilt berekenen die een veer uitoefent tijdens een bepaalde verplaatsing. Deze arbeid kan worden uitgedrukt als een integraal, waarbij de integrand de kracht van de veer is als functie van de verplaatsing. In veel gevallen kan deze kracht worden beschreven met behulp van een sinusfunctie, zoals sin 2x. De integraal van sin 2x stelt ons dan in staat om de totale arbeid te berekenen die de veer uitoefent.
Voordelen van de integraal van sin 2x
De integraal van sin 2x biedt verschillende voordelen:
- Toepasbaarheid in verschillende vakgebieden: Zoals eerder vermeld, is deze integraal relevant in de fysica, engineering, en andere disciplines die periodieke verschijnselen bestuderen.
- Vereenvoudiging van complexe berekeningen: Door gebruik te maken van substitutie kunnen we de integraal van sin 2x oplossen en gebruiken voor verdere berekeningen.
- Dieper begrip van trigonometrische functies: Het bestuderen van de integraal van sin 2x leidt tot een beter begrip van trigonometrische functies en hun eigenschappen.
De integraal van sin 2x berekenen
De integraal van sin 2x wordt berekend met behulp van de substitutiemethode. Hierbij substitueren we 2x met een nieuwe variabele, bijvoorbeeld u. We krijgen dan:
∫sin 2x dx = (1/2) ∫sin u du = -(1/2) cos u + C
Vervolgens substitueren we u terug naar 2x, wat ons de uiteindelijke oplossing geeft:
∫sin 2x dx = -(1/2) cos 2x + C
Veelgestelde vragen over de integraal van sin 2x
Hieronder vind je enkele veelgestelde vragen over de integraal van sin 2x:
- Wat is de afgeleide van -cos 2x? De afgeleide van -cos 2x is 2 sin 2x.
- Waar kan ik meer informatie vinden over integralen? Er zijn talloze online bronnen en textbooks beschikbaar die integralen en hun toepassingen behandelen. Zoek op "integralen" in je favoriete zoekmachine of raadpleeg een wiskundeboek op universitair niveau.
Conclusie
De integraal van sin 2x, hoewel ogenschijnlijk complex, opent de deur naar een fascinerend gebied van de wiskunde met brede toepassingen in verschillende disciplines. Door de eenvoud van de substitutiemethode te begrijpen, kunnen we deze integraal berekenen en gebruiken om complexe problemen op te lossen met betrekking tot periodieke verschijnselen. Van de beweging van een slinger tot de oscillatie van een veer, de integraal van sin 2x, en meer in het algemeen integralen van trigonometrische functies, spelen een cruciale rol in ons begrip van de wereld om ons heen. Door te blijven leren en verkennen, kunnen we de kracht van wiskundige concepten zoals deze ontsluiten en gebruiken om de mysteries van het universum te ontrafelen.
Voetbal dit weekend op tv de complete gids
Ontrafel het mysterie code cracker puzzles groundcover
Wordt het morgen terrasjesweer in hannover ontdek de weersvoorspelling
integral von sin 2 x - Khao Tick On
integral von sin 2 x - Khao Tick On
integral von sin 2 x - Khao Tick On
integral von sin 2 x - Khao Tick On
integral von sin 2 x - Khao Tick On
integral von sin 2 x - Khao Tick On
integral von sin 2 x - Khao Tick On
integral von sin 2 x - Khao Tick On
integral von sin 2 x - Khao Tick On
integral von sin 2 x - Khao Tick On
integral von sin 2 x - Khao Tick On
integral von sin 2 x - Khao Tick On
integral von sin 2 x - Khao Tick On
integral von sin 2 x - Khao Tick On
Chain Rule Formula Sheet - Khao Tick On