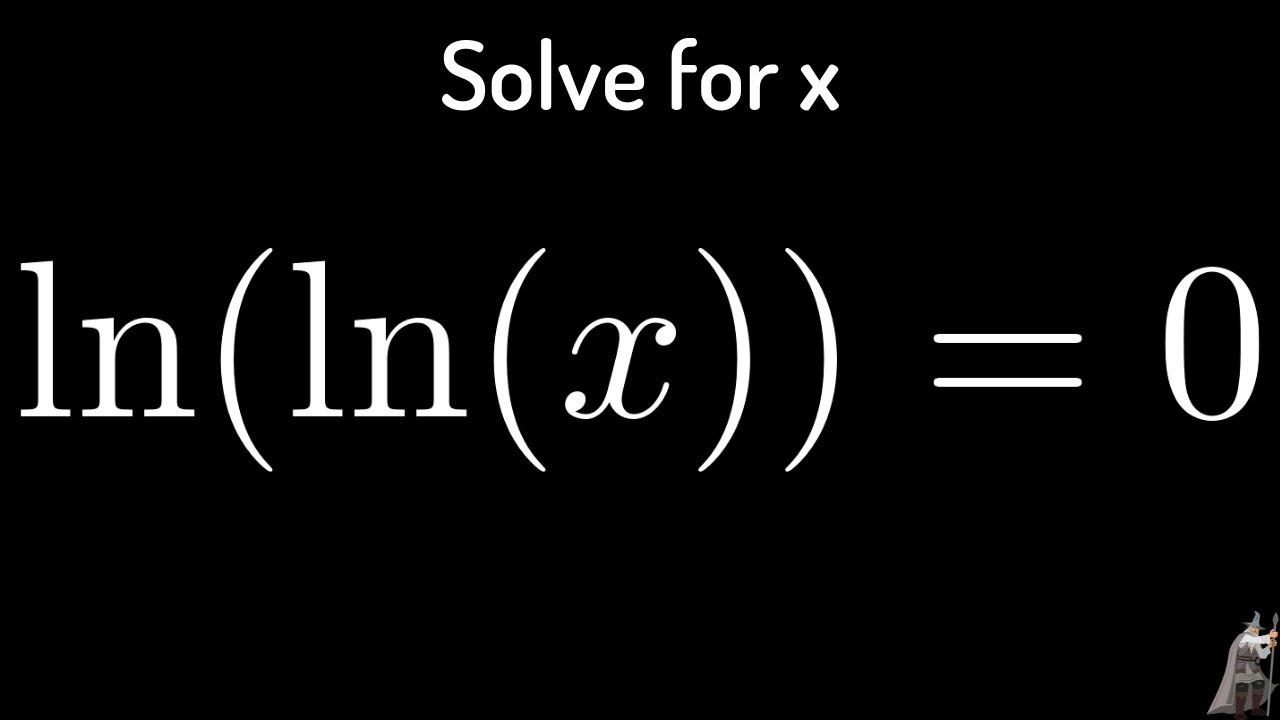De kracht van logaritmen: Ontrafel ln(x) + ln(x-5) = 1

04 Sep 2024
nl
Ann

Wiskunde. Voor velen een woord dat nostalgie oproept naar schoolbanken en verwarrende formules. Maar wist je dat wiskunde, en meer specifiek logaritmen, de sleutel kunnen zijn tot het ontrafelen van complexe vraagstukken in verschillende domeinen?

Neem bijvoorbeeld de vergelijking ln(x) + ln(x-5) = 1. Op het eerste gezicht lijkt dit misschien een abstracte formule, maar deze logaritmische vergelijking heeft toepassingen in gebieden zoals financiën, natuurkunde en informatica. Door de kracht van logaritmen te begrijpen, kunnen we deze vergelijking oplossen en de verborgen waarde van x onthullen.

Logaritmen werden in de 17e eeuw uitgevonden door John Napier als een manier om complexe vermenigvuldigingen en delingen te vereenvoudigen. Tegenwoordig worden ze gebruikt in diverse wetenschappelijke disciplines en vormen ze een essentieel onderdeel van geavanceerde wiskundige concepten.

De vergelijking ln(x) + ln(x-5) = 1 is een voorbeeld van hoe logaritmen ons kunnen helpen bij het oplossen van exponentiële problemen. In dit geval moeten we de eigenschappen van logaritmen gebruiken om de vergelijking te vereenvoudigen en op te lossen voor x.

Het begrijpen van logaritmen en hun eigenschappen is essentieel om dergelijke vergelijkingen succesvol te kunnen oplossen. Laten we eens dieper ingaan op de wereld van logaritmen en de stappen bekijken die nodig zijn om ln(x) + ln(x-5) = 1 op te lossen.

Logaritmen: Een korte introductie

Voordat we in de oplossing van onze vergelijking duiken, is het belangrijk om een basisbegrip van logaritmen te hebben. Een logaritme beantwoordt de vraag: "Tot welke macht moet ik een basis verheffen om een bepaald getal te krijgen?".

In ons voorbeeld is ln de natuurlijke logaritme, wat betekent dat de basis het getal e is (ongeveer 2.718). Dus ln(x) = 1 betekent: "Tot welke macht moet ik e verheffen om x te krijgen?".

De vergelijking ln(x) + ln(x-5) = 1 oplossen

Om deze vergelijking op te lossen, gebruiken we de volgende eigenschappen van logaritmen:

ln(a) + ln(b) = ln(a * b)

Met behulp van deze eigenschap kunnen we de vergelijking herschrijven als:

ln(x * (x-5)) = 1

Vervolgens gebruiken we de volgende eigenschap om de logaritme te verwijderen:

Als ln(a) = b, dan is a = e^b

Dit geeft ons:

x * (x-5) = e^1

Vereenvoudig de vergelijking:

x^2 - 5x - e = 0

Dit is nu een kwadratische vergelijking die we kunnen oplossen met de kwadratische formule. De oplossingen voor deze vergelijking geven ons de waarden van x die voldoen aan de oorspronkelijke logaritmische vergelijking.

Toepassingen van logaritmen

Zoals eerder vermeld, hebben logaritmen toepassingen in verschillende disciplines, waaronder:

Financiën: Berekening van samengestelde rente en investeringsgroei.
Natuurkunde: Modelleren van exponentiële groei en verval, zoals radioactief verval.
Informatica: Algoritmen en datastructuren, zoals binaire zoekbomen.

Conclusie

Logaritmen, hoewel ze op het eerste gezicht complex lijken, zijn krachtige wiskundige hulpmiddelen die ons helpen complexe problemen op te lossen. Door de eigenschappen van logaritmen te begrijpen, kunnen we vergelijkingen zoals ln(x) + ln(x-5) = 1 oplossen en de verborgen waarden ontsluiten. Deze vaardigheid is waardevol in diverse wetenschappelijke disciplines en heeft talloze toepassingen in de echte wereld. Door de kracht van logaritmen te benutten, kunnen we een dieper inzicht krijgen in de wereld om ons heen.

Trui korte mouw heren de veelzijdige stijlvolle keuze
Trending woorden de taal van de afgelopen twee jaar
Ontdek de wereld van gratis online codekrakers in nsw