Stel je voor: je bent een piraat op zoek naar een verborgen schat. Je hebt een oude kaart met vage aanwijzingen en mysterieuze symbolen. Gelukkig voor jou spreken de symbolen van driehoekige verhoudingen, de taal van sinus, cosinus en tangens! Deze trigonometrische functies, vaak afgekort als sin, cos en tan, zijn de sleutels tot het ontrafelen van hoeken, afstanden en de geheimen van de driehoek.
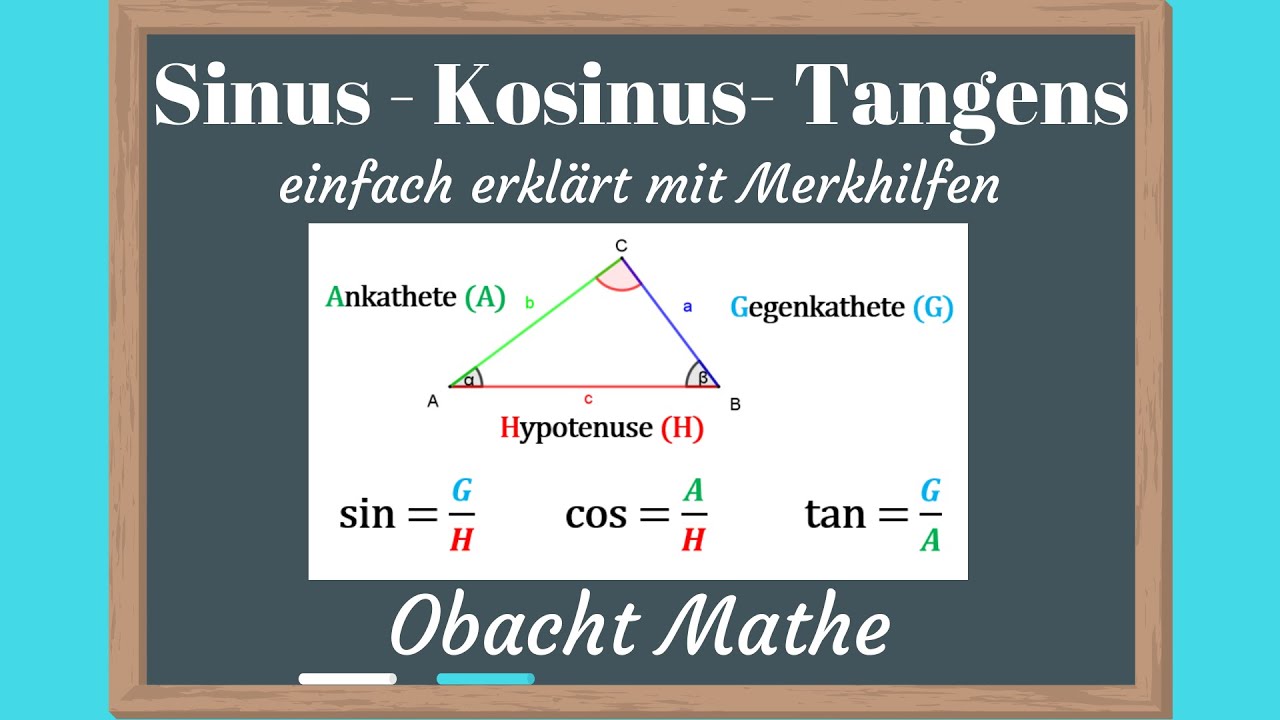
Sinus, cosinus en tangens, klinkt ingewikkeld? Eigenlijk zijn het gewoon verhoudingen tussen de zijden van een rechthoekige driehoek. Ze helpen ons de relatie tussen hoeken en zijden te begrijpen, en dat is ongelooflijk nuttig, niet alleen voor schatzoekende piraten!
De geschiedenis van deze trigonometrische functies gaat duizenden jaren terug, tot de oude Egyptenaren en Babyloniërs die ze gebruikten voor landmeting en astronomie. Griekse wiskundigen zoals Hipparchus en Ptolemaeus ontwikkelden de concepten verder, wat leidde tot de trigonometrie die we vandaag de dag kennen.
Maar waarom zijn sin, cos en tan zo belangrijk? Simpel gezegd, ze zijn overal! Van het berekenen van de hoogte van een gebouw tot het ontwerpen van bruggen en het voorspellen van de baan van een raket, trigonometrie en zijn functies spelen een cruciale rol in talloze vakgebieden, waaronder natuurkunde, engineering, architectuur en computergraphics.
Stel je voor dat je de hoogte van een boom wilt bepalen. Met behulp van een meetinstrument bepaal je de hoek tussen de grond en de top van de boom. Met de tangens van deze hoek en de afstand tot de boom, kun je de hoogte berekenen. Zie je, sin, cos en tan zijn niet alleen abstracte wiskundige concepten, maar praktische tools die ons helpen de wereld om ons heen te meten en te begrijpen.
Dus, de volgende keer dat je een rechthoekige driehoek tegenkomt, denk dan aan de kracht van sinus, cosinus en tangens. Deze trigonometrische helden staan klaar om je te helpen hoeken te temmen, afstanden te overbruggen en de mysteries van de driehoek te ontrafelen.
Voor- en nadelen van trigonometrie
Hoewel trigonometrie, inclusief sin, cos en tan, een krachtig hulpmiddel is, heeft het ook zijn voor- en nadelen.
| Voordelen | Nadelen |
|---|---|
| Veelzijdige toepassingen in diverse vakgebieden. | Vereist precisie in metingen en berekeningen. |
| Helpt bij het oplossen van complexe geometrische problemen. | Kan complex zijn voor beginners om te leren en toe te passen. |
| Fundamenteel voor geavanceerde wiskunde en natuurwetenschappen. | Vereist kennis van trigonometrische identiteiten en formules. |
Veelgestelde vragen over sin, cos en tan
1. Wat is het verschil tussen sin, cos en tan?
Sin, cos en tan zijn verhoudingen tussen verschillende zijden van een rechthoekige driehoek. Sin is de verhouding van de overstaande zijde tot de schuine zijde. Cos is de verhouding van de aanliggende zijde tot de schuine zijde. Tan is de verhouding van de overstaande zijde tot de aanliggende zijde.
2. Waar kan ik meer leren over trigonometrie?
Er zijn veel online bronnen en boeken beschikbaar die trigonometrie uitleggen, zoals Khan Academy en "Trigonometrie voor Dummies."
Kortom, sinus, cosinus en tangens zijn veel meer dan alleen wiskundige functies. Ze zijn de bouwstenen van onze kennis over driehoeken, hoeken en afstanden, en stellen ons in staat de wereld om ons heen op een dieper niveau te begrijpen. Dus, duik in de wereld van trigonometrie en ontdek de schoonheid en kracht van sin, cos en tan!
Hoeveel mensen zijn er op aarde een fascinerende blik op de wereldbevolking
De kracht en betekenis van sometimes love just aint enough lyrics tritt
Mannelijk onderzoek in beensteunen belang en procedure
wann sin cos tan - Khao Tick On
wann sin cos tan - Khao Tick On
Labeling Opposite Adjacent Hypotenuse Worksheet - Khao Tick On
wann sin cos tan - Khao Tick On
wann sin cos tan - Khao Tick On
Trigonometrie Erklärung mit Formeln und Beispielen - Khao Tick On
wann sin cos tan - Khao Tick On
wann sin cos tan - Khao Tick On
wann sin cos tan - Khao Tick On
wann sin cos tan - Khao Tick On
wann sin cos tan - Khao Tick On
wann sin cos tan - Khao Tick On
wann sin cos tan - Khao Tick On
wann sin cos tan - Khao Tick On
wann sin cos tan - Khao Tick On