Stel je voor: een wirwar van lijnen en punten op een grafiek. Hoe ontrafel je de verborgen wiskundige code achter deze visuele representatie? Het antwoord ligt in het bepalen van het functievoorschrift. Dit proces, ook wel het vinden van de vergelijking van de grafiek genoemd, is essentieel in diverse vakgebieden, van natuurkunde en economie tot data-analyse en engineering.
Het bepalen van een functievoorschrift van een grafiek is als het ontcijferen van een geheime taal. De grafiek vertelt een verhaal over de relatie tussen twee variabelen, en het functievoorschrift is de sleutel tot het begrijpen van dit verhaal. Het stelt ons in staat om voorspellingen te doen, trends te analyseren en de onderliggende principes te begrijpen die de gepresenteerde data bepalen.
De geschiedenis van het bepalen van functievoorschriften is nauw verweven met de ontwikkeling van de wiskunde zelf. Van de vroege meetkundige studies van de Grieken tot de moderne calculus, hebben wiskundigen steeds gezocht naar manieren om de relatie tussen variabelen te beschrijven en te kwantificeren. Het bepalen van een functievoorschrift is een krachtig instrument gebleken om complexe systemen te modelleren en te analyseren.
Een veelvoorkomend probleem bij het bepalen van een functievoorschrift is het onderscheiden van verschillende soorten functies, zoals lineaire, kwadratische, exponentiële en logaritmische functies. Elk type functie heeft zijn eigen karakteristieke vorm en vereist een specifieke aanpak om het functievoorschrift te bepalen. Het herkennen van het type functie is de eerste stap naar het succesvol afleiden van de vergelijking.
Het correct interpreteren van de grafiek is cruciaal. Belangrijke kenmerken zoals snijpunten met de assen, maxima en minima, en de algemene vorm van de grafiek geven waardevolle informatie over het functievoorschrift. Door deze kenmerken te identificeren en te analyseren, kunnen we de puzzelstukjes samenvoegen en het functievoorschrift reconstrueren.
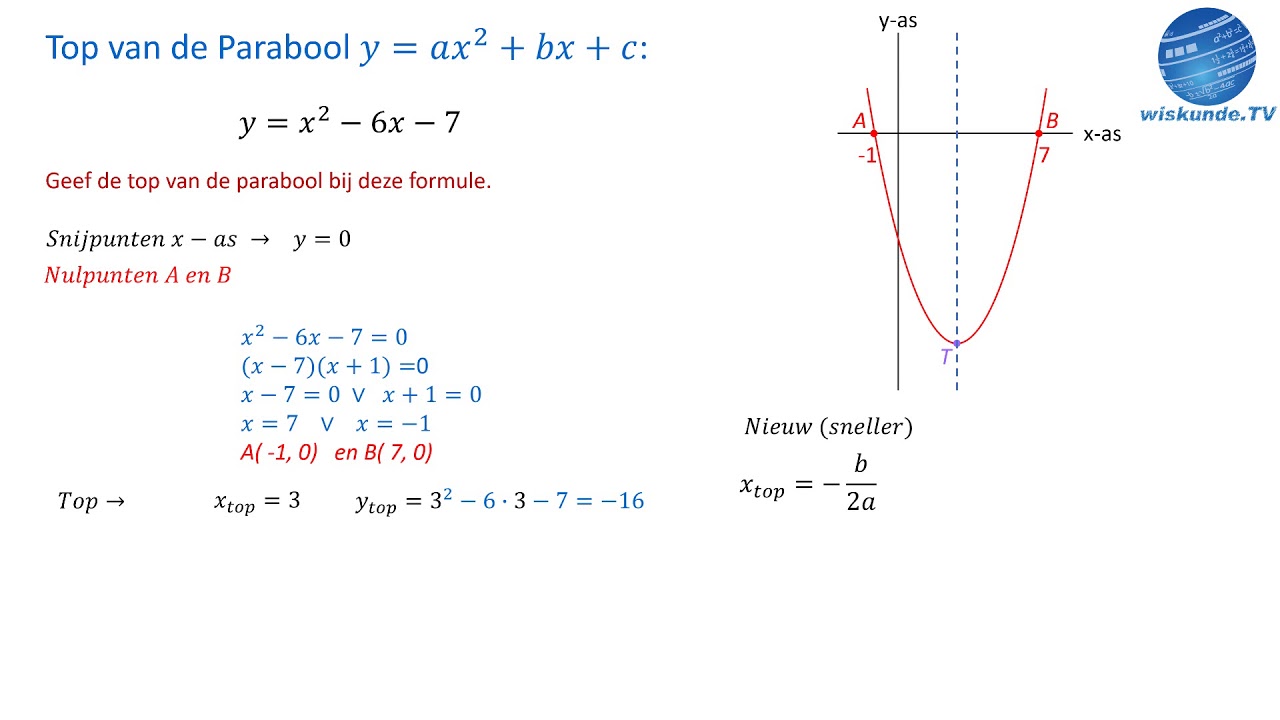
Een lineaire functie is te herkennen aan een rechte lijn. Het functievoorschrift heeft de vorm y = ax + b, waarbij a de richtingscoëfficiënt en b het snijpunt met de y-as is. Een parabool wijst op een kwadratische functie (y = ax² + bx + c). Exponentiële groei of verval is te herkennen aan een kromme die steeds sneller stijgt of daalt.
Voordelen van het bepalen van een functievoorschrift zijn: voorspellingen maken over toekomstige waarden, het modelleren van real-world scenario's en het optimaliseren van processen.
Een stap-voor-stap handleiding: 1. Identificeer het type functie. 2. Bepaal belangrijke punten op de grafiek. 3. Gebruik deze punten om de parameters van het functievoorschrift te berekenen.
Voor- en Nadelen van Functievoorschrift Bepalen
| Voordelen | Nadelen |
|---|---|
| Voorspellingen maken | Vereist nauwkeurige data |
| Modelleren van real-world scenario's | Kan complex zijn voor niet-lineaire functies |
Vijf beste praktijken: 1. Zorg voor accurate data. 2. Gebruik de juiste tools. 3. Controleer je resultaten. 4. Oefen regelmatig. 5. Vraag om hulp indien nodig.
FAQ: 1. Wat is een functievoorschrift? Antwoord: Een wiskundige formule die de relatie tussen twee variabelen beschrijft.
Conclusie: Het bepalen van een functievoorschrift is een essentiële vaardigheid met brede toepassingen. Door de methoden en technieken te beheersen, kunnen we waardevolle inzichten verkrijgen uit grafieken en data. Het is een krachtig instrument om de wereld om ons heen te begrijpen en te modelleren. Blijf oefenen en ontdek de magie van grafieken! Door het functievoorschrift te bepalen, ontrafelen we de verborgen wiskundige taal van data en openen we de deur naar een dieper begrip van de wereld om ons heen. Het stelt ons in staat om voorspellingen te doen, trends te analyseren en weloverwogen beslissingen te nemen op basis van concrete wiskundige modellen. Investeer tijd in het beheersen van deze vaardigheid, en je zult de vruchten plukken in diverse aspecten van je studie en carrière.
Voeding voor een gezonde maag tips en advies
Van zaadje tot smaakvolle snack paprikas kweken voor beginners
Wat is een filosoof ontdek de denker in jezelf
Differentiequotiënt bij grafiek - Khao Tick On
Leennormen in 2023 Dit is alles wat je moet weten - Khao Tick On
Hoe bepaal je een functievoorschrift aan de hand van een grafiek - Khao Tick On
functievoorschrift bepalen van een grafiek - Khao Tick On
functievoorschrift bepalen van een grafiek - Khao Tick On
Elementaire functies Verloopschema koppelen aan functievoorschrift - Khao Tick On
Het functievoorschrift van een eerstegraadsfunctie opstellen - Khao Tick On
functievoorschrift bepalen van een grafiek - Khao Tick On
functievoorschrift bepalen van een grafiek - Khao Tick On
Découvrir 47 imagen formule top - Khao Tick On
wiskunde Functievoorschrift bepalen als grafiek gegeven is - Khao Tick On
Hoe Bepaal Je Een Kpi - Khao Tick On
Vier Sjabloon Voor Het Bepalen Van Een Tabel Met Abonnementsopties Voor - Khao Tick On
functievoorschrift bepalen van een grafiek - Khao Tick On
functievoorschrift bepalen van een grafiek - Khao Tick On