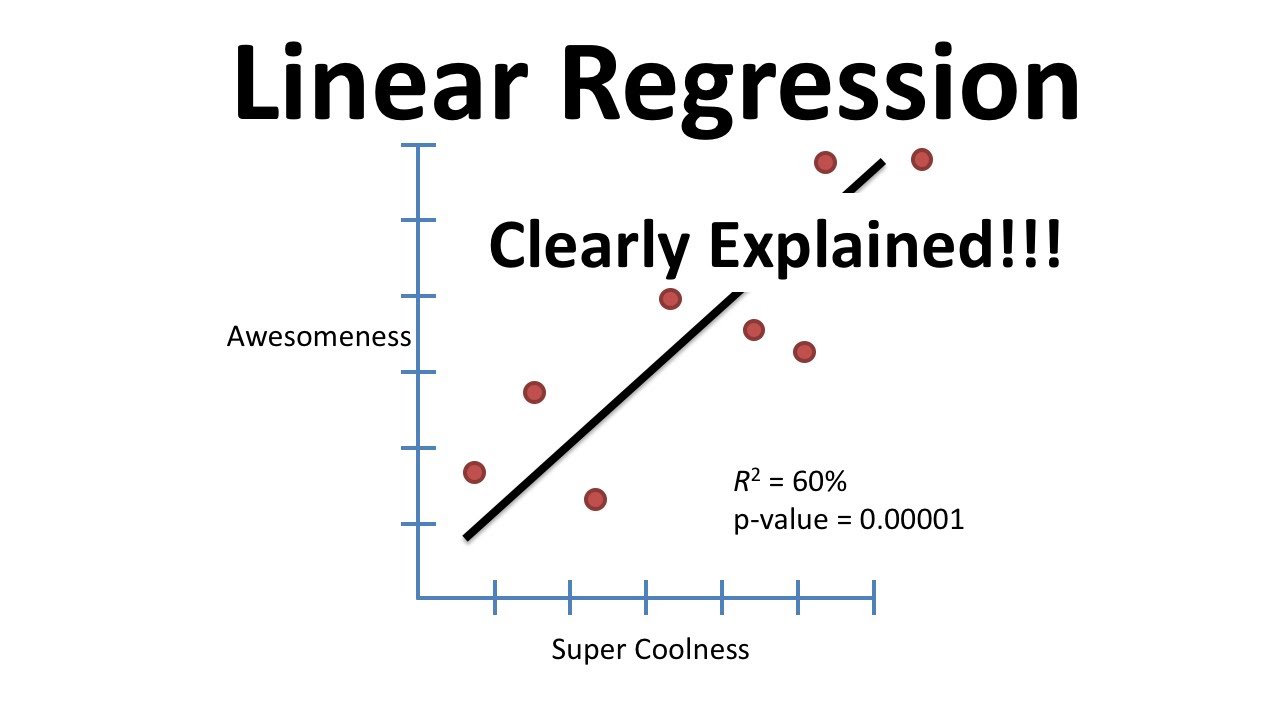
Kan een lineaire regressielijn krom zijn? Deze ogenschijnlijk simpele vraag opent een fascinerende wereld van statistische modellering die verder gaat dan de rechte lijnen van de standaard lineaire regressie. In veel gevallen is een rechte lijn niet voldoende om de relatie tussen variabelen accuraat te beschrijven. Denk bijvoorbeeld aan de groei van een plant: deze volgt geen rechte lijn, maar een meer complexe curve. Dit is waar niet-lineaire regressie, ofwel gekromde regressie, om de hoek komt kijken.
Lineaire regressie is een krachtige tool, maar de aanname van lineariteit beperkt de toepasbaarheid ervan. Wat als de relatie tussen je variabelen niet lineair is? Kunnen we dan nog steeds regressie gebruiken? Het antwoord is ja, door gebruik te maken van technieken die rekening houden met kromming. Dit opent de deur naar complexere en vaak realistischere modellen.
De behoefte aan gekromde regressie ontstond uit de observatie dat veel real-world fenomenen niet lineair zijn. Denk aan de relatie tussen de dosis van een medicijn en het effect ervan, of de relatie tussen temperatuur en de groeisnelheid van bacteriën. In zulke gevallen faalt een lineaire regressie om de data adequaat te modelleren.
Het concept van gekromde regressie is gebaseerd op het idee dat we de relatie tussen variabelen kunnen beschrijven met een wiskundige functie die niet lineair is. Dit kan een polynoom, een exponentiële functie, een logaritmische functie, of een combinatie daarvan zijn. Door de parameters van deze functies te schatten, kunnen we een curve vinden die zo goed mogelijk bij de data past.
Het doel van gekromde regressie is hetzelfde als dat van lineaire regressie: het modelleren van de relatie tussen variabelen om voorspellingen te kunnen doen. Het verschil zit hem in de vorm van de regressielijn. Waar lineaire regressie een rechte lijn gebruikt, gebruikt gekromde regressie een curve. Dit maakt het mogelijk om complexere relaties te modelleren en betere voorspellingen te doen in situaties waar een lineaire relatie niet voldoende is.
Een voorbeeld van gekromde regressie is polynomiale regressie. Hierbij wordt de relatie tussen de variabelen gemodelleerd met een polynoom, bijvoorbeeld een kwadratische of kubische functie. Een ander voorbeeld is exponentiële regressie, die vaak gebruikt wordt om groei of verval te modelleren.
Voor- en Nadelen van Gekromde Regressie
Helaas is er geen tabel functionaliteit beschikbaar in deze context. We beschrijven de voor- en nadelen hieronder.
Voordelen: Gekromde regressie biedt meer flexibiliteit en nauwkeurigheid bij het modelleren van niet-lineaire relaties. Het kan complexere patronen in data vastleggen en leidt vaak tot betere voorspellingen dan lineaire regressie in dergelijke gevallen.
Nadelen: Gekromde regressie kan complexer zijn om te implementeren en te interpreteren dan lineaire regressie. De keuze van de juiste niet-lineaire functie is cruciaal en vereist vaak domeinkennis. Overfitting kan ook een probleem zijn, waarbij het model te complex wordt en de ruis in de data leert in plaats van het onderliggende patroon.
Veelgestelde Vragen:
1. Wat is het verschil tussen lineaire en gekromde regressie? Gekromde regressie modelleert niet-lineaire relaties, terwijl lineaire regressie lineaire relaties modelleert.
2. Wanneer moet ik gekromde regressie gebruiken? Wanneer de relatie tussen je variabelen niet lineair is.
3. Welke soorten gekromde regressie zijn er? Voorbeelden zijn polynomiale, exponentiële en logaritmische regressie.
4. Hoe kies ik de juiste niet-lineaire functie? Dit vereist vaak domeinkennis en experimenteren.
5. Wat is overfitting? Wanneer het model te complex wordt en de ruis in de data leert.
6. Hoe kan ik overfitting voorkomen? Door technieken zoals cross-validatie te gebruiken.
7. Zijn er softwarepakketten voor gekromde regressie? Ja, de meeste statistische softwarepakketten bieden functionaliteit voor gekromde regressie.
8. Waar kan ik meer informatie vinden over gekromde regressie? Online bronnen, textbooks en statistische cursussen bieden meer informatie.
Conclusie: Gekromde regressie is een waardevolle tool voor het modelleren van niet-lineaire relaties. Hoewel het complexer kan zijn dan lineaire regressie, biedt het de flexibiliteit en nauwkeurigheid die nodig zijn om complexere patronen in data te ontrafelen. Door de juiste technieken te gebruiken en overfitting te vermijden, kan gekromde regressie leiden tot betere voorspellingen en een dieper begrip van de onderliggende relaties tussen variabelen. Begin vandaag nog met het verkennen van de mogelijkheden van gekromde regressie en ontdek de rijkdom die schuilgaat achter de data!
Hoeveel kiezen heeft een hond echt nodig ontdek het hier
Ontdek de charmes van noord holland noord jouw gids
Wat betekent regressie een eenvoudige uitleg
Linear Regression With Examples - Khao Tick On
Getting started with SGPLOT - Khao Tick On
Criterion Variable Definition Use and Examples - Khao Tick On
Multiple Linear Regression in R - Khao Tick On
How Can Linear Regression Be Performed In PySpark - Khao Tick On
Types Of Regression Curves - Khao Tick On
Explain Linear Regression With An Example - Khao Tick On
Reading excel linear regression equations - Khao Tick On
can linear regression lines be curved - Khao Tick On
Line Equation Of Regression at Russell Wilkins blog - Khao Tick On
can linear regression lines be curved - Khao Tick On
When to Use Linear Regression A Guide for Applying This Versatile - Khao Tick On
Comparing Regression Lines with Hypothesis Tests - Khao Tick On
How to Choose Between Linear and Nonlinear Regression - Khao Tick On
Vertical Horizontal E Diagonal - Khao Tick On