Het Mysterie van de Hoek: Ontdek de Binnenhoek van een Zeshoek

13 Aug 2024
nl
Ann

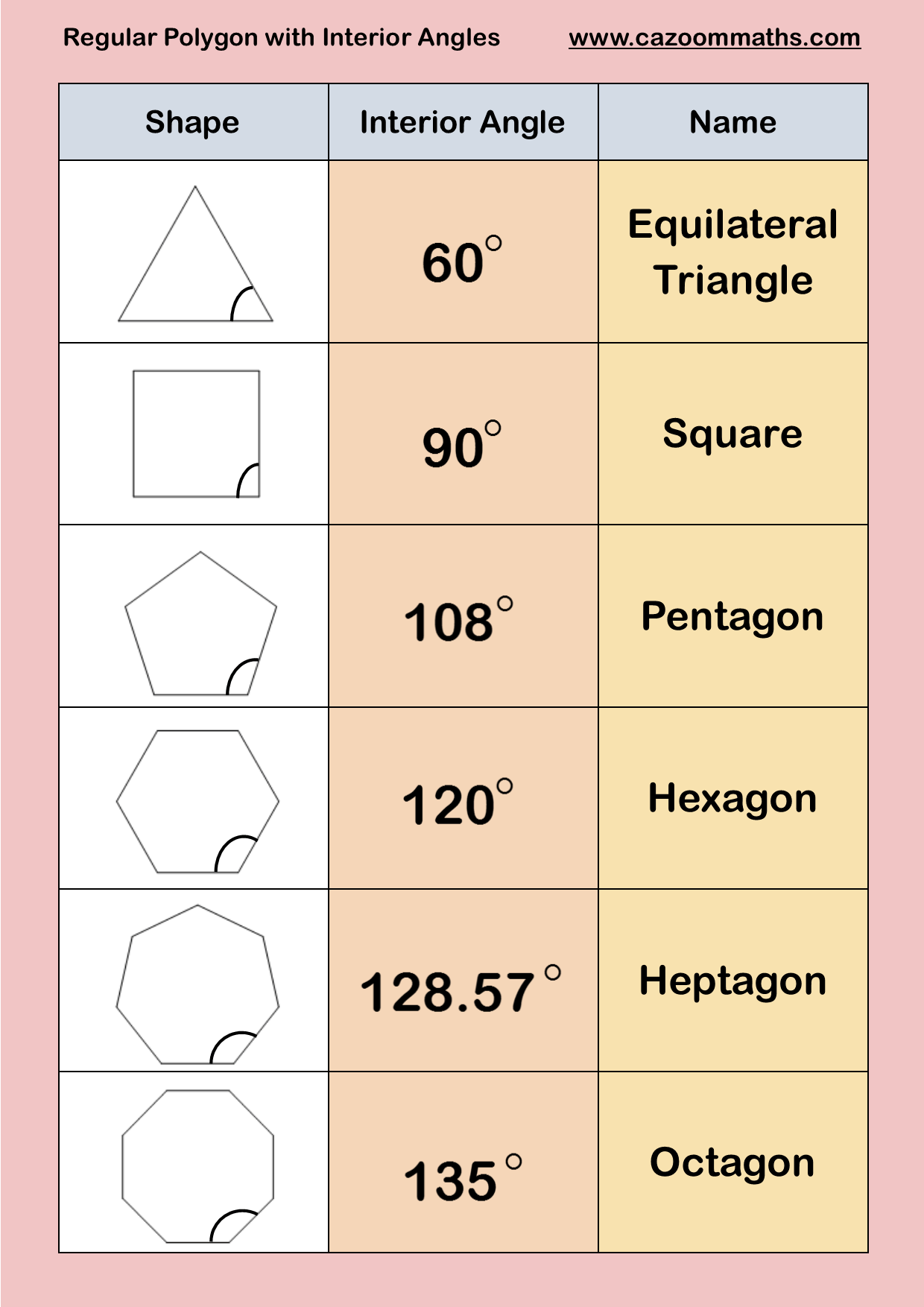
De wereld om ons heen zit vol geometrische vormen, en een van de meest intrigerende is de zeshoek. Van honingraten tot bestrating, zeshoeken zijn overal te vinden, en hun unieke eigenschappen maken ze fascinerend om te bestuderen. Eén van de belangrijkste kenmerken van een zeshoek is de binnenhoek. Maar wat is de binnenhoek van een zeshoek precies, en waarom is het zo belangrijk?

Laten we beginnen met de basis. Een zeshoek is een veelhoek met zes zijden en zes hoeken. De som van alle binnenhoeken van een zeshoek is altijd 720 graden. Dat betekent dat elke binnenhoek van een regelmatige zeshoek, waar alle zijden en hoeken gelijk zijn, 120 graden is.

Deze kennis over de binnenhoek van een zeshoek heeft een breed scala aan toepassingen in verschillende disciplines. Architecten gebruiken het om sterke en stabiele structuren te bouwen, terwijl grafisch ontwerpers het gebruiken om visueel aantrekkelijke ontwerpen te creëren. Zelfs in de natuur zien we het belang van de zeshoek, denk maar aan de efficiënte structuur van honingraten.

Het berekenen van de binnenhoek van een zeshoek is relatief eenvoudig. Je kunt de formule (n-2) * 180 / n gebruiken, waarbij 'n' het aantal zijden van de veelhoek is. In het geval van een zeshoek, zou de formule (6-2) * 180 / 6 zijn, wat resulteert in 120 graden.

Het begrijpen van de binnenhoek van een zeshoek is essentieel voor iedereen die te maken krijgt met geometrie, van studenten tot professionals. Het opent de deur naar een wereld van mogelijkheden op het gebied van ontwerp, constructie en meer.

Voor- en nadelen van het kennen van de binnenhoek van een zeshoek

Voordelen	Nadelen
Sterkere structuren bouwen	-
Efficiëntere ruimtelijke ordening	-
Verbeterde ontwerpestetiek	-

Beste Praktijken

Hier zijn enkele beste praktijken voor het werken met zeshoeken en hun binnenhoeken:

Gebruik nauwkeurige metingen om fouten te voorkomen.
Visualiseer de zeshoek en zijn hoeken voor een beter begrip.
Pas de juiste formules toe voor nauwkeurige berekeningen.
Gebruik hulpmiddelen zoals gradenbogen en software voor geometrische constructies.
Controleer uw werk om de nauwkeurigheid te garanderen.

Veelgestelde Vragen

1. Wat is de som van de binnenhoeken van een zeshoek?
De som van de binnenhoeken van een zeshoek is altijd 720 graden.

2. Hoe bereken je de binnenhoek van een regelmatige zeshoek?
Je kunt de formule (n-2) * 180 / n gebruiken, waar 'n' het aantal zijden is. Voor een zeshoek is dit (6-2) * 180 / 6 = 120 graden.

3. Waar worden zeshoeken in het dagelijks leven gebruikt?
Zeshoeken worden gebruikt in honingraten, bestrating, tegels, bouten en moeren, en meer.

4. Wat is het belang van de binnenhoek van een zeshoek in de architectuur?
De binnenhoek van 120 graden zorgt voor sterkte en stabiliteit in constructies.

5. Kan de binnenhoek van een zeshoek variëren?
Ja, de binnenhoeken van een onregelmatige zeshoek kunnen variëren, maar de som blijft altijd 720 graden.

6. Welke software kan ik gebruiken om zeshoeken te tekenen en te meten?
Er zijn verschillende softwareprogramma's beschikbaar, zoals GeoGebra, AutoCAD en SketchUp.

7. Wat is de relatie tussen de binnenhoek en de buitenhoek van een zeshoek?
De binnenhoek en de buitenhoek van een zeshoek zijn supplementair, wat betekent dat ze samen 180 graden vormen.

8. Waar kan ik meer informatie vinden over zeshoeken en hun eigenschappen?
Je kunt online bronnen raadplegen, zoals Wikipedia, wiskundeboeken en educatieve websites.

Tips en Trucs

Onthoud deze tips bij het werken met zeshoeken:

Oefening baart kunst: Hoe meer je oefent met het tekenen en meten van zeshoeken, hoe beter je het onder de knie krijgt.
Visualiseer: Probeer je de zeshoek en zijn hoeken voor te stellen om de concepten beter te begrijpen.
Zoek hulp: Aarzel niet om hulp te vragen aan leraren, professoren of online bronnen als je vastloopt.

Kortom, de binnenhoek van een zeshoek is een fundamenteel concept in de geometrie met brede toepassingen in verschillende disciplines. Door de eigenschappen en berekeningen ervan te begrijpen, kunnen we de wereld om ons heen beter waarderen en gebruiken. Dus blijf nieuwsgierig, blijf verkennen en de fascinerende wereld van zeshoeken zal zich voor je openen!

Wie regeert de onderwereld ontdek de koning der hel
De fascinerende reis van zaadje tot boom ontdek het ontstaan van bomen
Hoe ziet dat eruit ontdek de impact en mogelijkheden