Heb je je ooit afgevraagd hoe je de hoekgrootte van een zeshoek kunt berekenen? Of waarom deze geometrische vorm zo belangrijk is in de natuur en architectuur? In deze blogpost duiken we in de fascinerende wereld van zeshoeken en ontrafelen we de geheimen van hun unieke eigenschappen.
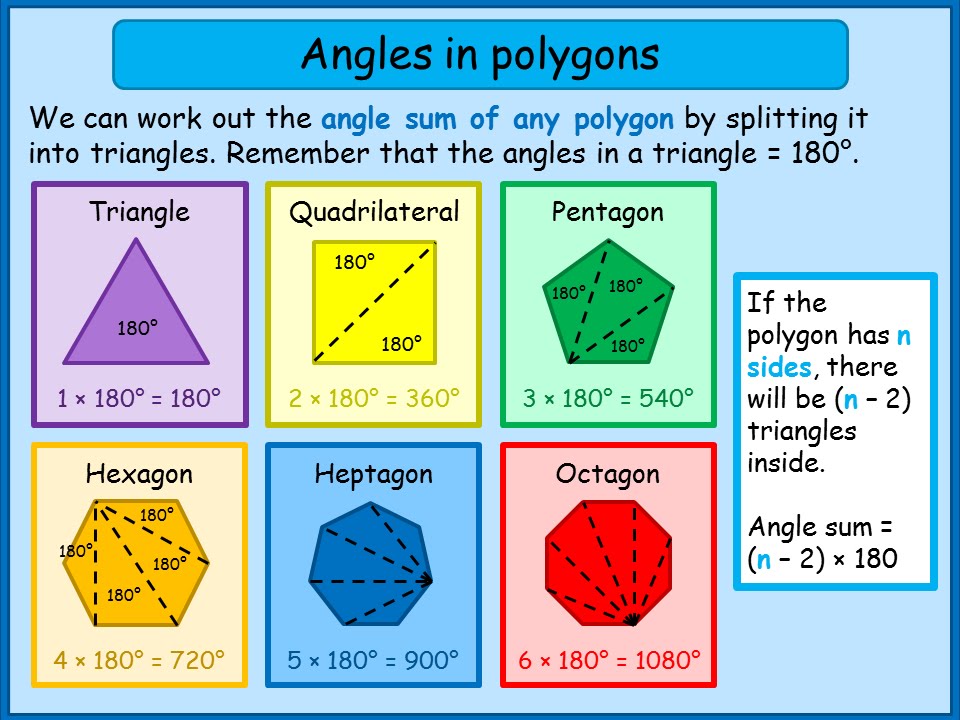
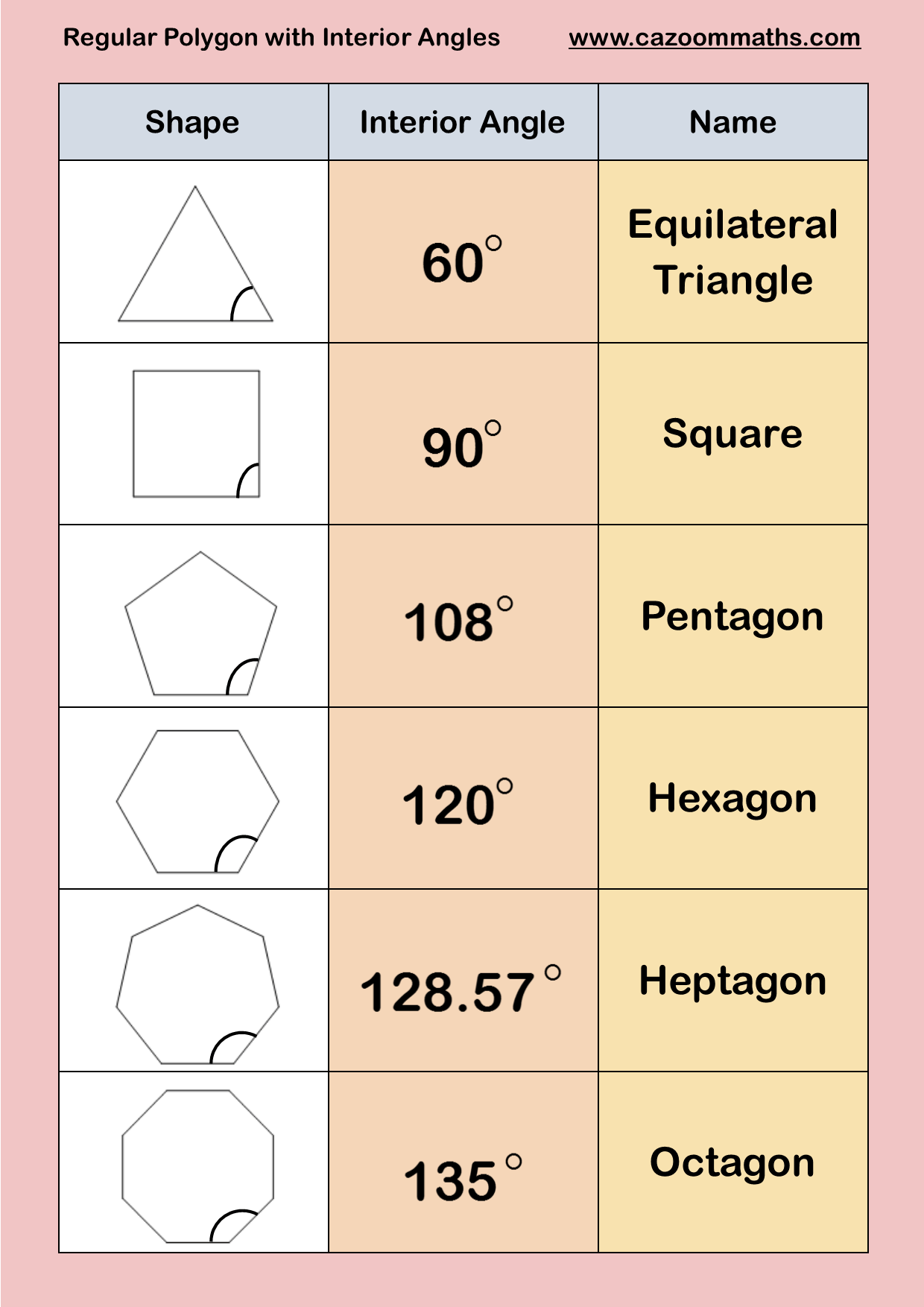
Een zeshoek is een veelhoek met zes zijden en zes hoeken. De som van de binnenhoeken van een zeshoek is altijd 720 graden. Dit betekent dat elke binnenhoek van een regelmatige zeshoek, waarbij alle zijden en hoeken gelijk zijn, 120 graden meet.
Het bepalen van de hoekgrootte van een zeshoek is niet alleen een wiskundige oefening, maar heeft ook praktische toepassingen. Denk bijvoorbeeld aan het ontwerpen van honingraten, het bouwen van stabiele constructies en het creëren van prachtige mozaïekpatronen.
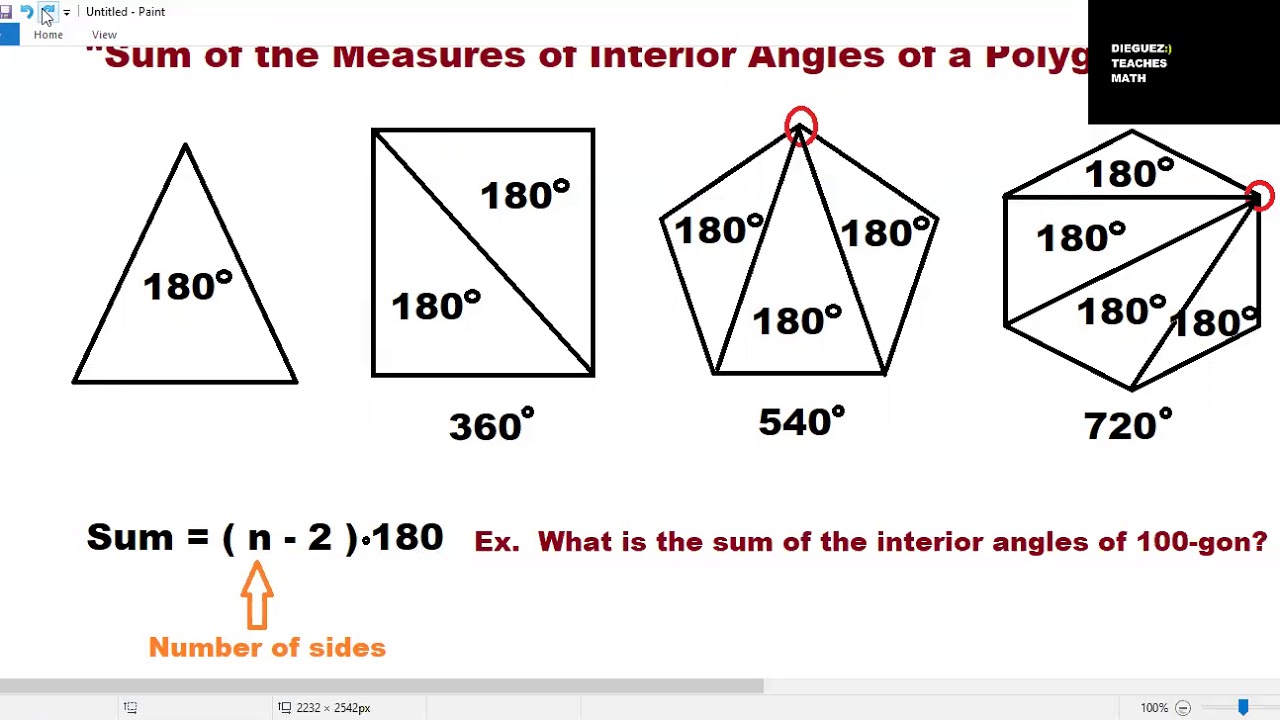
De formule om de grootte van elke binnenhoek van een regelmatige veelhoek, inclusief een zeshoek, te berekenen, is als volgt:
Hoekgrootte = (n - 2) * 180° / n
Waarbij 'n' het aantal zijden van de veelhoek is. Voor een zeshoek (n=6) krijgen we:
Hoekgrootte = (6 - 2) * 180° / 6 = 120°
Deze formule is afgeleid van het feit dat elke veelhoek kan worden opgedeeld in (n-2) driehoeken, en de som van de hoeken in elke driehoek is 180 graden.
Voordelen van het begrijpen van hoekgroottes in zeshoeken:
Het kunnen berekenen en begrijpen van de hoekgroottes in zeshoeken biedt talloze voordelen, waaronder:
- Verhoogd ruimtelijk inzicht: Het helpt je om vormen en patronen beter te visualiseren en te begrijpen, wat essentieel is in vakgebieden zoals wiskunde, kunst en design.
- Verbeterde probleemoplossende vaardigheden: Het daagt je uit om logisch na te denken en wiskundige concepten toe te passen om praktische problemen op te lossen, bijvoorbeeld bij het bepalen van de benodigde materialen voor een bouwproject.
- Verhoogde waardering voor de natuur en technologie: Je zult versteld staan van hoe zeshoeken voorkomen in honingraten, sneeuwvlokken en zelfs in de structuur van bepaalde moleculen.
Praktische toepassingen van hoekgroottes in zeshoeken:
De kennis van hoekgroottes in zeshoeken is essentieel in diverse toepassingen, zoals:
- Architectuur: Zeshoekige structuren staan bekend om hun stabiliteit en efficiënt gebruik van materialen. Ze worden gebruikt in bruggen, gebouwen en zelfs in de constructie van voetbaldoelen.
- Grafisch ontwerp: Zeshoeken creëren aantrekkelijke en dynamische patronen die vaak worden gebruikt in logo's, achtergronden en webdesign.
- Natuurwetenschappen: Van de zeshoekige structuur van honingraten tot de moleculaire structuur van benzeen, zeshoeken spelen een belangrijke rol in de natuur en scheikunde.
Conclusie
De hoekgrootte van een zeshoek is een fascinerend gegeven met talloze toepassingen. Of je nu een student, professional of gewoon nieuwsgierig bent, het begrijpen van dit concept opent een wereld van mogelijkheden om de wereld om ons heen beter te begrijpen en te waarderen. Van architectuur tot natuur, zeshoeken bewijzen keer op keer hun elegantie, efficiëntie en schoonheid.
Work Out Exterior Angles Of A Polygon - Khao Tick On
How To Know If A Polygon Is Regular Or Not - Khao Tick On
Exterior Angles Of A Polygon Examples - Khao Tick On
measure of each interior angle of a hexagon - Khao Tick On
measure of each interior angle of a hexagon - Khao Tick On
measure of each interior angle of a hexagon - Khao Tick On
measure of each interior angle of a hexagon - Khao Tick On
measure of each interior angle of a hexagon - Khao Tick On
measure of each interior angle of a hexagon - Khao Tick On
measure of each interior angle of a hexagon - Khao Tick On
measure of each interior angle of a hexagon - Khao Tick On
measure of each interior angle of a hexagon - Khao Tick On
measure of each interior angle of a hexagon - Khao Tick On
measure of each interior angle of a hexagon - Khao Tick On
Angles In A Pentagon - Khao Tick On