Stel je voor: je bent een architect die de perfecte hoek voor een dak wil berekenen, of een game-ontwikkelaar die realistische bewegingen in je game wil creëren. In beide gevallen heb je te maken met trigonometrie, een tak van de wiskunde die zich bezighoudt met de relaties tussen de hoeken en zijden van driehoeken. En binnen deze fascinerende wereld spelen de trigonometrische functies sinus (sin), cosinus (cos) en tangens (tan) een cruciale rol.
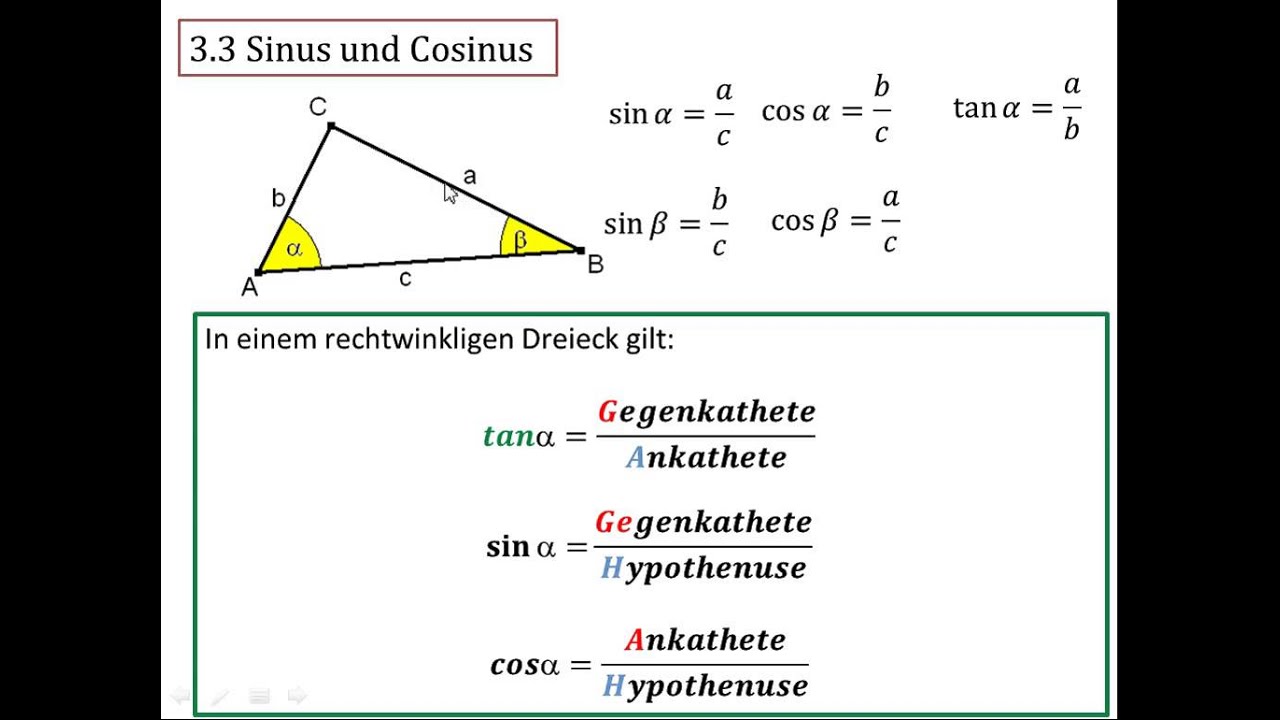
Maar wat is nu precies de relatie tussen deze drie? Simpel gezegd, de tangens van een hoek in een rechthoekige driehoek is gelijk aan de verhouding tussen de overstaande zijde en de aanliggende zijde. Maar we kunnen tan ook uitdrukken in termen van sin en cos. Zo is de tangens van een hoek gelijk aan de sinus van die hoek gedeeld door de cosinus van die hoek: tan(hoek) = sin(hoek) / cos(hoek). Deze ogenschijnlijk eenvoudige formule opent een wereld aan mogelijkheden om complexe geometrische problemen op te lossen.
De geschiedenis van trigonometrie gaat terug tot de oude beschavingen van Egypte en Babylonië, waar men de basisprincipes gebruikte voor landmeting en astronomie. De Griekse astronoom Hipparchus wordt beschouwd als de vader van de trigonometrie, omdat hij de eerste tabellen met trigonometrische waarden opstelde. Sindsdien heeft trigonometrie zich ontwikkeld tot een onmisbaar instrument in tal van wetenschappelijke disciplines, van natuurkunde en engineering tot muziek en computergraphics.
Een van de belangrijkste voordelen van het uitdrukken van tan in termen van sin en cos is dat het ons in staat stelt om trigonometrische identiteiten te vereenvoudigen en te manipuleren. Deze identiteiten zijn wiskundige vergelijkingen die altijd waar zijn, ongeacht de waarde van de hoek. Door gebruik te maken van de relatie tussen tan, sin en cos kunnen we complexe trigonometrische uitdrukkingen vereenvoudigen tot meer beheersbare vormen. Dit is vooral handig bij het oplossen van vergelijkingen en het bewijzen van stellingen.
Een ander voordeel is dat het ons inzicht geeft in de onderliggende geometrische relaties. Door tan te beschouwen als de verhouding tussen sin en cos, kunnen we de tangens van een hoek interpreteren in termen van de verhoudingen tussen de zijden van een rechthoekige driehoek. Dit kan ons helpen om problemen op een meer intuïtieve manier te visualiseren en op te lossen.
De toepassingen van tan, sin en cos in de echte wereld zijn legio. Ingenieurs gebruiken deze functies om bruggen en gebouwen te ontwerpen, natuurkundigen gebruiken ze om de beweging van objecten te beschrijven en computerwetenschappers gebruiken ze om realistische 3D-graphics te creëren. Of je nu een student bent die worstelt met wiskunde, of een professional die zijn of haar kennis van trigonometrie wil opfrissen, het begrijpen van de relatie tussen tan, sin en cos is essentieel.
Voor- en nadelen van tan als sin/cos:
| Voordeel | Nadeel |
|---|---|
| Vereenvoudigt trigonometrische identiteiten | Kan complexer lijken bij directe berekeningen |
| Geeft inzicht in geometrische relaties | Vereist kennis van zowel sin als cos |
Kortom, de wereld van trigonometrie mag dan op eerste gezicht complex lijken, de relatie tussen tan, sin en cos is een sleutelbegrip dat de deur opent naar een dieper begrip van driehoeken en hun eigenschappen. Of je nu een student, professional of gewoon nieuwsgierig bent naar de wonderen van wiskunde, het ontdekken van de geheimen van tan, sin en cos zal je horizon zeker verbreden en je een krachtig instrument geven om de wereld om je heen te begrijpen en te manipuleren.
Ontdek de intelligente en energieke australische kelpie jouw trouwe metgezel
Ds l w van der meij een diepgaande blik
Sterren op het doek bekijken ontdek de magie
tan als sin und cos - Khao Tick On
tan als sin und cos - Khao Tick On
Winkel Aus Cosinus Berechnen - Khao Tick On
File:Sine Cosine Exponential qtl1.svg - Khao Tick On
tan als sin und cos - Khao Tick On
tan als sin und cos - Khao Tick On
tan als sin und cos - Khao Tick On
tan als sin und cos - Khao Tick On
Relationship between sine, cosine and exponential function - Khao Tick On
File:Sine Cosine Exponential qtl1.svg - Khao Tick On
tan als sin und cos - Khao Tick On
tan als sin und cos - Khao Tick On
tan als sin und cos - Khao Tick On
tan als sin und cos - Khao Tick On
Ableitung von Funktionen, Sinus, Cosinus, Logarithmus, e - Khao Tick On