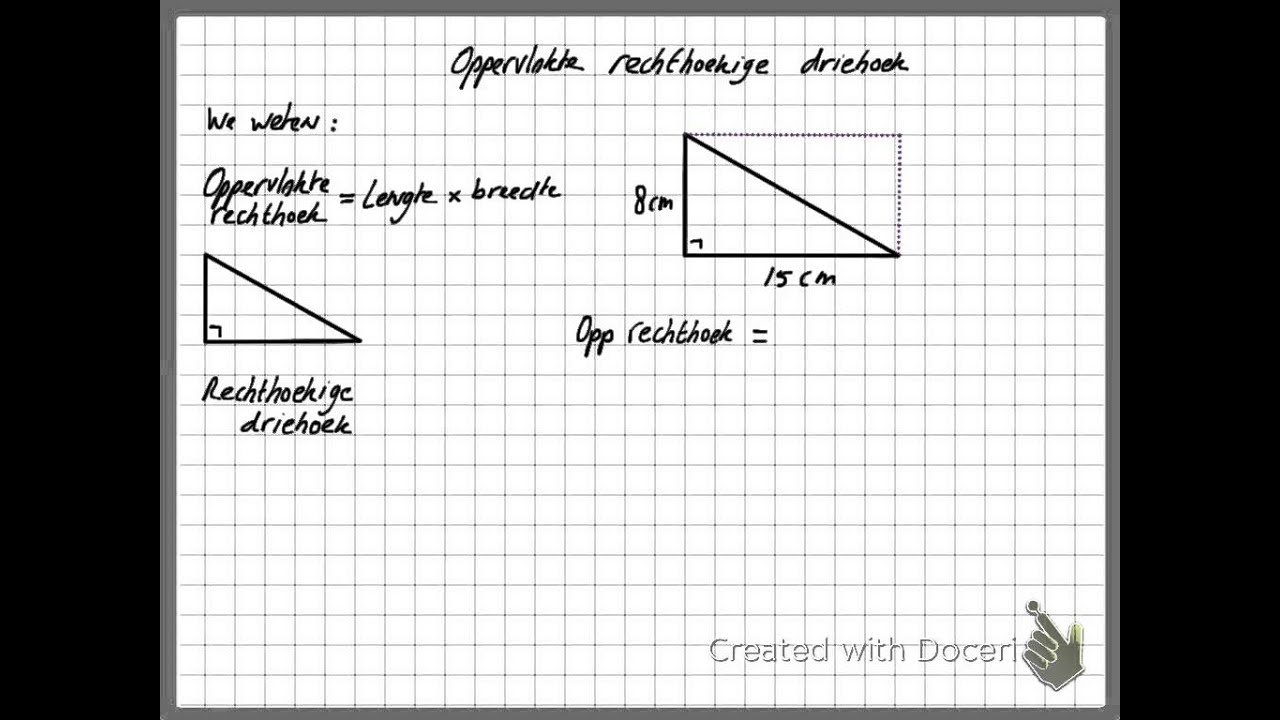
Hoe bereken je snel en gemakkelijk de oppervlakte van een rechthoekige driehoek? Deze vraag komt vaak voor in de wiskunde en heeft praktische toepassingen in verschillende vakgebieden, van constructie tot design. Het begrijpen van de formule voor de oppervlakte van een rechthoekige driehoek is essentieel voor iedereen die met geometrie werkt.
De oppervlakte van een rechthoekige driehoek is de ruimte die de driehoek inneemt. Een rechthoekige driehoek is een driehoek met één rechte hoek (90 graden). De zijden die de rechte hoek vormen, noemen we de rechthoekszijden. De formule om de oppervlakte te berekenen is verrassend eenvoudig: (rechthoekszijde 1 x rechthoekszijde 2) / 2. Deze formule is afgeleid van de formule voor de oppervlakte van een rechthoek, die lengte x breedte is. Een rechthoekige driehoek is namelijk precies de helft van een rechthoek.
Het concept van oppervlakteberekening gaat terug tot de oude beschavingen, zoals de Egyptenaren en Babyloniërs, die deze kennis gebruikten voor landmeting en bouwprojecten. De Griekse wiskundige Pythagoras leverde een belangrijke bijdrage aan de geometrie, inclusief de stelling van Pythagoras, die nauw verwant is aan rechthoekige driehoeken. Zijn werk legde de basis voor ons moderne begrip van driehoeken en hun eigenschappen.
Het berekenen van de oppervlakte van een rechthoekige driehoek is cruciaal in verschillende disciplines. In de architectuur wordt het gebruikt voor het ontwerpen van daken, ramen en andere structurele elementen. In de techniek is het essentieel voor het berekenen van materiaalbehoeften en belastingen. Zelfs in de kunst en het design speelt het een rol bij het creëren van visueel aantrekkelijke composities.
Een veelvoorkomend probleem bij het berekenen van de oppervlakte is het correct identificeren van de rechthoekszijden. Zorg ervoor dat je de twee zijden gebruikt die de rechte hoek vormen, en niet de schuine zijde (de hypotenusa). Verwar de formule ook niet met die van een gewone driehoek, die een andere formule gebruikt (basis x hoogte) / 2.
De formule is: Oppervlakte = (rechthoekszijde 1 x rechthoekszijde 2) / 2. Stel, rechthoekszijde 1 is 4 cm en rechthoekszijde 2 is 6 cm. Dan is de oppervlakte (4 x 6) / 2 = 12 cm².
Voordelen:
1. Eenvoudig te gebruiken: De formule is simpel en gemakkelijk te onthouden.
2. Breed toepasbaar: Vanuit architectuur tot tuinieren, de formule is overal bruikbaar.
3. Fundamenteel voor verdere geometrie: Begrijpen van deze formule is de basis voor complexere geometrische berekeningen.
Stap-voor-stap handleiding:
1. Identificeer de rechthoekszijden.
2. Vermenigvuldig de lengtes van de rechthoekszijden.
3. Deel het resultaat door 2.
Voor- en Nadelen
| Voordelen | Nadelen |
|---|---|
| Eenvoudige formule | Alleen toepasbaar op rechthoekige driehoeken |
Veelgestelde vragen:
1. Wat is een rechthoekige driehoek? Een driehoek met een hoek van 90 graden.
2. Wat is de formule? (rechthoekszijde 1 x rechthoekszijde 2) / 2.
3. Wat zijn rechthoekszijden? De zijden die de rechte hoek vormen.
4. Wat is de eenheid van oppervlakte? Vierkante eenheden (cm², m², etc.).
5. Kan ik deze formule gebruiken voor andere driehoeken? Nee, alleen voor rechthoekige driehoeken.
6. Wat is de stelling van Pythagoras? a² + b² = c² (waar a en b de rechthoekszijden zijn en c de hypotenusa).
7. Hoe vind ik de rechthoekszijden? Zoek de hoek van 90 graden, de zijden die deze hoek vormen zijn de rechthoekszijden.
8. Wat is het verschil met de oppervlakte van een rechthoek? De oppervlakte van een rechthoekige driehoek is de helft van de oppervlakte van een rechthoek met dezelfde rechthoekszijden als lengte en breedte.
Tips en trucs: Gebruik een rekenmachine voor nauwkeurige berekeningen. Teken de driehoek om de rechthoekszijden te visualiseren.
De formule voor de oppervlakte van een rechthoekige driehoek is een fundamenteel concept in de geometrie met brede toepassingen in diverse vakgebieden. Het begrijpen en correct toepassen van deze formule is essentieel voor iedereen die met wiskunde en ruimtelijke berekeningen werkt. Van architecten tot ingenieurs en kunstenaars, de formule biedt een eenvoudige en effectieve manier om de oppervlakte van rechthoekige driehoeken te berekenen. Door de eenvoud van de formule en de praktische toepasbaarheid is het een onmisbaar instrument voor iedereen die met vormen en afmetingen werkt. Blijf oefenen met verschillende voorbeelden en je zult merken dat het berekenen van de oppervlakte van een rechthoekige driehoek een fluitje van een cent wordt. Verken de wereld van de geometrie en ontdek de kracht van deze eenvoudige, maar krachtige formule.
Twee nummers op een telefoon ontdek de wereld van dual sim
Jumbo supermarkt dichtbij jouw boossechappen oplossing
Die heute show gemist geen paniek zo kijk je de aflevering terug
Omtrek en oppervlakte van vlakke figuren Formules - Khao Tick On
Oppervlakte van een driehoek in functie van de lengte van drie - Khao Tick On
oppervlakte rechthoekige driehoek formule - Khao Tick On
Formule Driehoek Oppervlakte Formule - Khao Tick On
Hoe bereken je een driehoek - Khao Tick On
Oppervlakte van vlakke figuren Formules - Khao Tick On
oppervlakte rechthoekige driehoek formule - Khao Tick On
oppervlakte rechthoekige driehoek formule - Khao Tick On
oppervlakte rechthoekige driehoek formule - Khao Tick On
Formule Cirkel Oppervlakte Formule - Khao Tick On
oppervlakte rechthoekige driehoek formule - Khao Tick On
oppervlakte rechthoekige driehoek formule - Khao Tick On
Hoe bereken ik de oppervlakte Oefeningen Uitleg - Khao Tick On
oppervlakte rechthoekige driehoek formule - Khao Tick On
Omtrek en oppervlakte Formules - Khao Tick On