The Unexpected Elegance of Trigonometry in Everyday Life

12 Sep 2024
us
Ann

Have you ever paused to admire a beautifully designed building, its sleek lines reaching towards the sky? Or perhaps found yourself captivated by the harmonious melodies of a symphony orchestra? While seemingly disparate, these experiences are subtly unified by a common thread: the elegant principles of trigonometry. Often relegated to the confines of textbooks and classrooms, trigonometry might seem like an abstract mathematical concept with little relevance to our daily lives. However, this couldn't be further from the truth. In reality, trigonometry is woven into the very fabric of our world, silently orchestrating everything from the construction of skyscrapers to the navigation of airplanes, and even influencing the music we listen to.

The journey of trigonometry began centuries ago, its origins tracing back to the ancient civilizations of Egypt and Mesopotamia. These early mathematicians were driven by practical needs – to survey land, construct pyramids, and map the stars. Through meticulous observation and calculation, they laid the groundwork for what we now know as trigonometry, establishing the fundamental relationships between angles and sides of triangles. As centuries passed, the torch of trigonometric knowledge was passed on, finding new life and application in the hands of Greek, Indian, and Islamic scholars. Each culture contributed its own unique insights, expanding the vocabulary and applications of this powerful mathematical tool.

Fast forward to today, and the influence of trigonometry is more pervasive than ever. Architects and engineers rely on its principles to design safe and aesthetically pleasing structures, calculating angles and distances with precision. Surveyors use trigonometry to map land, create topographical maps, and determine property boundaries. Astronomers peer deep into the cosmos, using trigonometric calculations to measure the vast distances between celestial objects. The music we listen to is also deeply intertwined with trigonometry. The harmonious interplay of sound waves, the very essence of musical harmony, can be understood and manipulated using trigonometric functions.

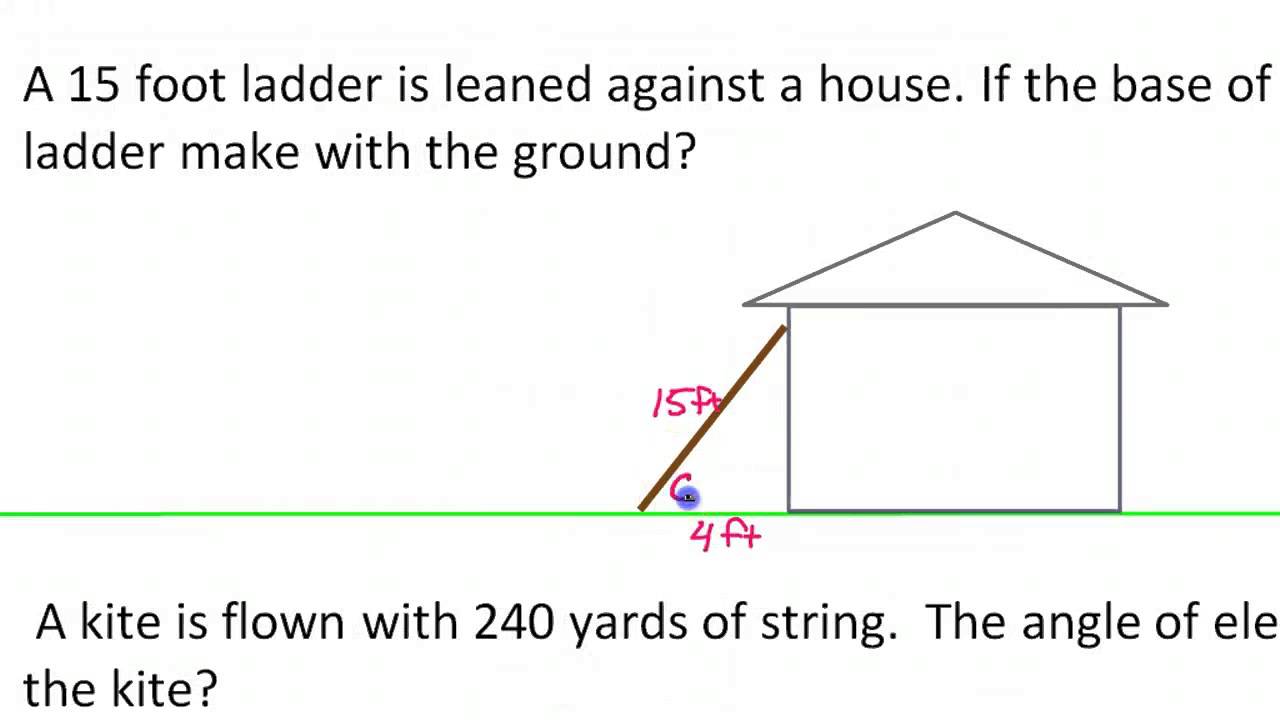
One of the beauties of trigonometry lies in its ability to simplify complex geometric problems. By breaking down shapes into triangles, we can utilize trigonometric ratios – sine, cosine, and tangent – to solve for unknown sides and angles. Imagine needing to determine the height of a tall tree. Using only a simple protractor and a measuring tape, along with a dash of trigonometry, we can accomplish this feat. By measuring the angle of elevation to the top of the tree from a known distance, and applying the tangent function, we unlock the secret of the tree's height.

Beyond these specific examples, the true power of understanding trigonometry lies in cultivating a deeper appreciation for the interconnectedness of our world. It equips us with the tools to analyze and interpret patterns, to make sense of the physical space around us, and to appreciate the subtle mathematical harmonies that underpin our universe.

As we've explored, trigonometry is far from being a dusty, abstract concept confined to textbooks. Its influence is deeply woven into the fabric of our world, silently shaping our experiences and enabling remarkable feats of engineering, navigation, and artistic expression. From the towering skyscrapers that define our cities to the captivating melodies that resonate within our souls, trigonometry is there, subtly orchestrating the symphony of our lives. So, the next time you encounter a beautiful building, listen to a piece of music, or simply gaze up at the stars, take a moment to appreciate the hidden elegance of trigonometry at play.

Marion county ohio mugshots
Blast processing revisiting the genesis of sonic the hedgehog
Unlocking the secrets of po box 7251 sioux falls sd